This article decries the use of "disorder" in teaching beginning students about thermodynamic entropy. It is cautionary rather than proscriptive about "disorder" being used warily as a device for assessing entropy change in advanced work or among professionals.1
To aid students in visualizing an increase in entropy many elementary chemistry texts use artists' before-and-after drawings of groups of "orderly" molecules that become "disorderly". This has been an anachronism ever since the ideas of quantized energy levels were introduced in elementary chemistry. "Orderly-disorderly" seems to be an easy visual support but it can be so grievously misleading as to be characterized as a failure-prone crutch rather than a truly reliable, sturdy aid.2
After mentioning the origin of this visual device in the late 1800s and listing some errors in its use in modern texts, I will build on a recent article by Daniel F. Styer. It succinctly summarizes objections from statistical mechanics to characterizing higher entropy conditions as disorderly (1). Then after citing many failures of "disorder" as a criterion for evaluating entropy — all educationally unsettling, a few serious, I will urge the abandonment of order-disorder in introducing entropy to beginning students. Although it seems plausible, it is vague and potentially misleading, a non-fundamental description that does not point toward calculation or elaboration in elementary chemistry, and an anachronism since the introduction of portions of quantum mechanics in first-year textbooks.3
Entropy's nature is better taught by first describing its dependence on the dispersion of energy (in classic thermodynamics), and the distribution of energy among a large number of molecular motions, relatable to quantized states, microstates (in molecular thermodynamics).4 Increasing amounts of energy dispersed among molecules result in increased entropy that can be interpreted as molecular occupancy of more microstates. (High-level first-year texts could go further to a page or so of molecular thermodynamic entropy as described by the Boltzmann equation.).
As is well-known, in 1865 Clausius gave the name "entropy" to a unique quotient for the process of a reversible change in thermal energy divided by the absolute temperature (2). He could properly focus only on the behavior of chemical systems as macro units because in that era there was considerable doubt even about the reality of atoms. Thus, the behavior of molecules or molecular groups within a macro system were totally a matter of conjecture (as Rankine unfortunately demonstrated in postulating "molecular vortices") (3). Later in the nineteenth century, but still prior to the development of quantum mechanics, the greater "disorder" of a gas at high temperature compared to its distribution of velocities at a lower temperature was chosen by Boltzmann to describe its higher entropy (4). However, "disorder" was a crutch, i.e., it was a contrived support for visualization rather than a fundamental physical or theoretical cause for a higher entropy value. Others followed Boltzmann's lead; Helmholtz in 1882 called entropy "Unordnung" (disorder) (5), and Gibbs Americanized that description with "entropy as mixed-up-ness", a phrase found posthumously in his writings (6) and subsequently used by many authors.
Most general chemistry texts today still lean on this conceptual crutch of order-disorder either slightly with a few examples or as a major support that too often fails by leading to extreme statements and over extrapolation. The most egregious errors in the past century of associating entropy with disorder have occurred simply because disorder is a common language word with non-scientific connotations. Whatever Boltzmann meant by it, there is no evidence that he used disorder in any sense other than strict application to molecular energetics. But over the years, popular authors have learned that scientists talked about entropy in terms of disorder, and thereby entropy has become a code word for the "scientific" interpretation of everything disorderly from drunken parties to dysfunctional personal relationships,5 and even the decline of society.6
Of course, chemistry instructors and authors would disclaim any responsibility for such absurdities. They would insist that they never have so misapplied entropy, that they used disorder only as a visual or conceptual aid for their students in understanding the spontaneous behavior of atoms and molecules, entropy-increasing events.
But it was not a social scientist or a novelist — it was a chemist — who discussed entropy in his textbook with "things move spontaneously [toward] chaos or disorder".7 Another wrote, "Desktops illustrate the principle [of] a spontaneous tendency toward disorder in the universe…".7 It is nonsense to describe the "spontaneous behavior" of macro objects in this way: that things like sheets of paper, immobile as they are, behave like molecules despite the fact that objects' actual movement is non-spontaneous and is due to external agents such as people, wind, and earthquake. That error has been adequately dismissed (7). The important point here is that this kind of mistake is fundamentally due to a focus on disorder rather than on the correct cause of entropy change, energy flow toward dispersal. Such a misdirected focus leads to the kind of hyperbole one might expect from a science-disadvantaged writer, "Entropy must therefore be a measure of chaos", but this quote is from an internationally distinguished chemist and author.7, 8
Entropy is not disorder. Entropy is not a measure of disorder or chaos. Entropy is not a driving force. Energy's diffusion, dissipation, or dispersion in a final state compared to an initial state is the driving force in chemistry. Entropy is the index of that dispersal within a system and between the system and its surroundings.4 In thermodynamics, entropy change is a quotient that measures the quantity of the unidirectional flow of thermal energy by DS > Dq/T. An appropriate paraphrase would be "entropy change measures energy's dispersion at a stated temperature". This concept of energy dispersal is not limited to thermal energy transfer between system and surroundings. It includes redistribution of the same amount of energy in a system, e.g., when a gas is allowed to expand into a vacuum container, resulting in a larger volume. In such a process where dq is zero, the total energy of the system has become diffused over a larger volume and thus an increase in entropy is predictable. (Some call this an increase in configurational entropy.)(1)
From a molecular viewpoint, the entropy of a system depends on the number of distinct microscopic quantum states, microstates, that are consistent with the system's macroscopic state. (The expansion of a gas into an evacuated chamber mentioned above is found, by quantum mechanics, to be an increase in entropy that is due to more microstates being accessible because the spacing of energy levels decreases in the larger volume.) The general statement about entropy in molecular thermodynamics can be: "Entropy measures the dispersal of energy among molecules in microstates. An entropy increase in a system involves energy dispersal among(2a) more microstates in the system's final state than in its initial state." It is the basic sentence to describe entropy increase in gas expansion, mixing, crystalline substances dissolving, phase changes and the host of other phenomena now inadequately described by "disorder" increase.
In the next section the molecular basis for thermodynamics is briefly stated. Following it are ten examples to illustrate the confusion that can be engendered by using "disorder" as a crutch to describe entropy in chemical systems.
The four paragraphs to follow include a paraphrase of Styer's article, "Insight into entropy" in the American Journal of Physics (1).9
In statistical mechanics, many microstates usually correspond to any single macrostate. (That number is taken to be one for a perfect crystal at absolute zero.) A macrostate is measured by its temperature, volume, and number of molecules; a group of molecules in microstates ("molecular configurations", a microcanonical ensemble) by their energy, volume, and number of molecules.
In a microcanonical ensemble the entropy is found simply by counting: One counts the number W of microstates that correspond to the given macrostate,10 and computes the entropy of that macrostate by Boltzmann's relationship, S = kB ln W, where kB is Boltzmann's constant.11
Clearly, S is high for a macrostate when many microstates correspond to that macrostate, whereas it is low when few microstates correspond to the macrostate. In other words, the entropy of a macrostate measures the number of ways in which a system can be different microscopically (i.e., molecules be very different in their energetic distribution) and yet still be a member of the same macroscopic state.
To put it mildly, considerable skill and wise interpretation are required to translate this verbal definition into quantitative expressions for specific situations. (Professor Styer's article describes some conditions for such evaluations and calculations.) Nevertheless, the straightforward and thoroughly established conclusion is that the entropy of a chemical system is a function of the multiplicity of molecular energetics. From this, it is equally straightforward that an increase in entropy is due to an increase in the number of microstates in the final macrostate. This modern description of a specifiable increase in the number of microstates (or better, groups of microstates)(2b) contrasts greatly with any common definition of "disorder", even though "disorder" was the best Boltzmann could envision in his time for the increase in gas velocity distribution.
There is no need today to confuse students with nineteenth century ad hoc ideas of disorder or randomness and from these to create pictures illustrating "molecular disorder". Any valid depiction of a spontaneous entropy change must be related to energy dispersal on a macro scale or to an increase in the number of accessible microstates on a molecular scale.
This example, a trivial non-issue to chemists who see phenomena from a molecular standpoint and always in terms of system plus surroundings, can be confusing to naive adults or beginning chemistry students who have heard that "entropy is disorder". It is mentioned only to illustrate the danger of using the common language word disorder.
An ordinary glass bowl containing water that has cracked ice floating in it portrays macro disorder, irregular pieces of a solid and a liquid. Yet, the spontaneous change in the bowl contents is toward an apparent order: In a few hours there will be only a homogeneous transparent liquid. Of course, the dispersal of energy from the warmer room surroundings to the ice in the system is the cause of its melting. However, to the types of individuals mentioned who have little knowledge of molecular behavior and no habit pattern of evaluating possible energy interchange between a system and its surroundings, this ordinary life experience can be an obstacle to their understanding. It will be especially so if disorder as visible non-homogeneity or mixed-up-ness is fixed in their thinking as signs of spontaneity and entropy increase. Thus, in some cases, with some groups of people, this weak crutch can be more harmful than helpful.
A comparable dilemma (to those who have heard only that "entropy is disorder" and that it spontaneously increases over time) is presented when a vegetable oil is shaken with water to make a disorderly emulsion of oil in water (8b). However (in the absence of an emulsifier), this metastable mixture will soon separate into two "orderly" layers. Order to disorder? Disorder to order? These are not fundamental criteria nor driving forces. It is the chemical and thermodynamic properties of oil and of water that determine such phase separation.
The following examples constitute significantly greater challenges than do the foregoing to the continued use of disorder in teaching about entropy.

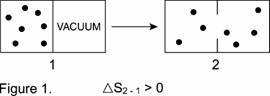
When this spontaneous process is portrayed in texts with little dots representing molecules as in Figure 1, the use of "disorder" as an explanation to students for an entropy increase becomes either laughable or an exercise in tortuous rationalization. Today's students may instantly visualize a disorderly mob crowded into a group before downtown police lines. How is it that the mob becomes more disorderly if its individuals spread all over the city? The professor who responds with his/her definition must realize that he/she is particularizing a common word that has multiple meanings and even more implications. As was well stated:"We cannot therefore always say that entropy is a measure of disorder without at times so broadening the definition of "disorder" as to make the statement true by [our] definition only"(10).
Furthermore, the naïve student who has been led to focus on disorder increase as an indicator of entropy increase, and is told that ΔS is positive in Figure 1, could easily be confused in several ways. For example, there has been no change in the number of particles (or the temperature or q), so the student may conclude that entropy increase is intensive (besides the Clausius equation's being "erroneous", with a q = 0). The molecules are more spread out, so entropy increase looks like it is related to a decrease in concentration. Disorder as a criterion of entropy change in this example is worse than even a double-edged sword.
How much clearer it is to say simply that if molecules can move in a larger volume, this allows them to disperse their original energy more widely in that larger volume and thus their entropy increases. Alternatively, from a molecular viewpoint, in the larger volume there are more closely spaced — and therefore more accessible — microstates(3) for translation without any change in temperature.
In texts or classes where the quantum mechanical behavior of a particle in a box has been treated, the expansion of a gas with N particles can be described in terms of microenergetics. Far simpler for other classes is the example of a particle of mass m in a one-dimensional box of length L (where n is an integer, the quantum number, and h is Planck's constant): E = (n2h2)/(8mL2). If L is increased, the possible energies of the single particle get closer together. As a consequence, if there were many molecules rather than one particle, the density of the states available to them would increase with increasing L. This result holds true in three dimensions, the microstates become closer together, more accessible to molecules within a given span of energy.(4)
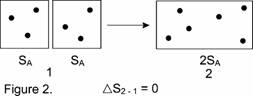
Does any text that uses disorder in describing entropy change dare to put dots representing ideal gas molecules in a square, call that molecular representation disorderly, attach it to another similar square while eliminating the barrier lines, and call the result more disorderly, as in Figure 2? Certainly the density of the dots is unchanged in the new rectangle, so how is the picture more "disorderly"? In the preceding Example 2, if the instructor used a diagram involving molecular-dot arrangements, an implication any student could draw was that entropy change was like a chemical concentration change; entropy was therefore an intensive property. Yet, here in Example 3, the disorder-description of entropy must be changed to the opposite, to be extensive! With just these two simple examples, the crutch of disorder for categorizing entropy to beginning students can be seen to be broken — not just weak.
(Generally, as in this example, entropy is extensive. However, its additivity is not true for all systems (11a).
Helium atoms move much more rapidly than do those of krypton at the same temperature. Therefore, any student who has been told about disorder and entropy would predict immediately that a mole of helium would have a higher entropy than a mole of krypton because the helium atoms are so much more wildly ricocheting around in their container. That of course is wrong. Again, disorder proves to be a broken crutch to support deductions about entropy. Helium has a standard state entropy of 126 J/K mol whereas krypton has the greater S0, 164 J/K mol.
The molecular thermodynamic explanation is not obvious but it fits with energetic considerations whereas "disorder" does not. The heavier krypton actually does move more slowly than helium. However, krypton's greater mass, and greater range of momenta, results in closer spacing of energy levels and thus more microstates for dispersing energy than in helium.
NOTE: In this example and the one that follows, students are confused about associating entropy with order arising in a system only if they fail to consider what is happening in the surroundings (and that this includes the solution in which a crystalline solid is precipitating, prior to any subsequent transfer to the environment). Thus, they should repeatedly be reminded to think about any observation as part of the whole, the system plus its surroundings. When orderly crystals form spontaneously in these two examples, focusing on entropy change as energy dispersal to or from a system and its surroundings is clearly a superior view to one that depends on a superficiality like disorder in the system (even plus the surroundings). Example 7 is introduced only as a visual illustration of the failure of order-disorder as a reliable indicator of entropy change in a complex system.
Students who believe that spontaneous processes always yield greater disorder could be somewhat surprised when shown a demonstration of supercooled liquid water at many degrees below 00 C. The students have been taught that liquid water is disorderly compared to solid ice. When a seed of ice or a speck of dust is added, crystallization of some of the liquid is immediate. Orderly solid ice has spontaneously formed from the disorderly liquid.
Of course, thermal energy is evolved in the process of this thermodynamically metastable state changing to one that is stable. Energy is dispersed from the crystals, as they form, to the solution and thus the final temperature of the crystals of ice and liquid water are higher than originally. This, the instructor ordinarily would point out as a system-surroundings energy transfer. However, the dramatic visible result of this spontaneous process is in conflict with what the student has learned about the trend toward disorder as a test of spontaneity. Such a picture might not take a thousand words of interpretation from an instructor to be correctly understood by a student, but they would not be needed at all if the misleading relation of disorder with entropy had not been mentioned.
In many texts the dissolving of a crystalline solid in water is shown in a drawing as an increase in disorder among the ions or molecules in the solid and the drawing is said to illustrate an increase in entropy. In general, solutions are described as having a higher entropy than a crystalline solid in contact with water prior to any dissolution. Thus, a demonstration involving a supersaturated solution of sodium sulfate is unsettling to students who have been erroneously assured that spontaneous processes always move in the direction of increased disorder.
Either by jarring the flask containing the clear supersaturated solution at room temperature or by adding a crystal of sodium sulfate, the flask of "disorderly" solution spontaneously becomes filled with "orderly" crystals. Furthermore, the flask becomes cool. A student who has been conditioned to think in terms of order and disorder is not just confused but doubly confused: Orderly crystals have formed spontaneously and yet the temperature has dropped. Disorder has not only spontaneously changed to order but the change was so favored energetically that thermal energy was taken from the surroundings. ("Triply confused" might describe a student who is focused on order and disorder rather than on energetics and the chemistry in comparing Examples 5 and 6. In 5, the temperature rises when supercooled water crystallizes to ice because of thermal energy evolution (and energy dispersal to the surroundings) during crystal formation in a monocomponent liquid-solid system. In 6, crystallization of the sodium sulfate from aqueous solution results in a temperature drop because anhydrous sodium sulfate is precipitating; it is one of the minority of solutes that decrease in solubility with temperature increase. Thus, energy is dispersed to the solid system from the solution surroundings as the sodium sulfate forms from the metastable supersaturated solution. No convoluted, verbalism-dependent discussion of order-disorder is needed.
If students are shown drawings of the arrangements of rod-like molecules that form liquid crystals, they would readily classify the high temperature liquid "isotropic" phase as disorderly, the liquid "nematic" (in which the molecules are oriented but their spatial positions still scattered) as somewhat orderly, and the liquid "smectic" phase (wherein the molecules are not only oriented but tending to be in sheets or planes) as very orderly. The solid crystal, of course, would be rated the most orderly.
Subsequently, the students would yawn when told that a hot liquid crystal (isotropic) of a particular composition (with the acronym of 6OCB) changes into a nematic phase when the liquid is cooled. Disorderly to more orderly, what can be more expected than that when liquid crystals drop in temperature? Cooling the nematic phase then yields the even more orderly smectic phase. Yawn. Continuing to cool the 6OCB now forms the less orderly nematic phase again. The students may not instantly become alert at hearing this, but most instructors will: The pictorially less orderly nematic phase at some temperatures has more entropy than the smectic and at some temperatures may have less entropy.
Entropy is not dependent on disorder.
Recent publications have thoroughly established that order in groups of small particles, easily visible under a low-power microscope, can be caused spontaneously by Brownian-like movement of smaller spheres that in turn is caused by random molecular motion (13-16). These findings therefore disprove the old qualitative idea that disorder or randomness is the inevitable outcome of molecular motion, a convincing argument for abandoning the word disorder in discussing the subject of entropy.
Only a selected few references are given here. Their proof of the fact that entropy can increase in a process that at the same time increases geometric order was the clinching evidence for a prominent expert in statistical mechanics to discard order-disorder in his writing about entropy.12
Students and professors are usually confident that they can recognize disorder whenever they see it. Styer found that their confidence was misplaced when he tested their evaluation of "lattice gas models", patterns used in a wide variety of studies of physical phenomena (1). Lattice gas models can be in the form of a two-dimensional grid in which black squares may be placed. With a grid of 1225 empty spaces and 169 black squares to be put on it in some arrangement, Styer showed two examples to students and professors and asked them which "had the greater entropy", in obtaining their estimation of the more disorderly arrangement.
Most of those questioned were wrong; they saw "patterns" in the configuration that belonged to the class that would have the greater entropy not less — the configuration they should have called more disorderly if they truly could discern disorder from the appearance of a single "still" from an enormous stack of such "stills".
Calculations by Styer evaluated similar diagrams in a book about entropy by a prominent chemist. It has been widely-read by scientists and non-scientists alike. His results showed that five diagrams that were checked were invalid; they had probably been selected to appear disorderly but were statistically not truly random. Humans see patterns everywhere. Conversely, we can easily be fooled into concluding that we are seeing disorder and randomness where there are actually complex patterns.
Besides the failures of disorder as a guide to entropy, a profound objection to the use of disorder as a tool to teach entropy to beginners is its dead-end nature for them. It does not lead to any quantitative treatment of disorder-entropy relations on their level. It does not serve as a foundation for more complex theoretical treatments that explain chemical behavior to them. (Complex applications of order-disorder are not pertinent to the first-year chemistry course, nor to most physical chemistry texts and courses.1)
In contrast, a simple qualitative emphasis on entropy increase as the result of the dispersal of energy generally and the occupancy of more microstates specifically(5) constitutes an informal introduction to statistical mechanics and quantum mechanics. Later, this can be seen as a natural beginning to substantial work in physical chemistry. A focus on energy flow as the key to understanding changes in entropy is not a dead-end or an end in itself. It is seminal for future studies in chemistry.
Entropy is seen by many as a mystery, partly because of the baggage it has accumulated in the popular view, partly because its calculation is frequently complex, partly because it is truly an unusual thermodynamic quantity — not just a direct measurement, but a quotient of two measurements: thermal flow divided by temperature. Qualitative statements such as the following about why or how molecules can absorb precise amounts of macro thermal flow, and about entropy change in a few basic processes, can remove much of the confusion in the minds of students about entropy even if the calculations may not be any easier.
In a macro view the "entropy" of a substance at T is actually an entropy change from 0 K to T, the integral (from 0 K to T) of the thermal energy divided by T that has been dispersed within it from some source. It is thus an index of the energy that has diffused into the particular type of substance over that temperature range. (Heat capacity is a specific "per degree" property; entropy is the integration of that kind of dissipation of energy within a substance from absolute zero, including phase changes and other energy-involving transitions.)
In a micro view the quantity of energy that can be dispersed in the molecules of a substance is clearly due to their state — warm solids have absorbed or "soaked up" more energy than cold solids because their molecules vibrate back and forth more in the warm solid crystals. Liquids have dissipated or "soaked up" more than solids due to their moving more freely and rotating (and perhaps vibrating within themselves). Even more energy has been dispersed in gases than liquids in occupying some of the even greater number of microstates that are available(6) in the gaseous state. With this kind of view (rather than a focus on disorder), the entropy of molecules in a solid, liquid or gas phase loses its mystery. The amount of energy dispersed within a substance at T (measured by its entropy) is the amount its molecules need to move normally at that temperature, i.e. to occupy energetic states consistent with that temperature. In reactions, the ΔS between products and reactants measures precisely how much more or how much less energy/T is required for the existence of the products than the original reactants at the stated T.
The expansion of a gas in a vacuum has been described in an initial section of this article and in Example 2. It is especially important because it is troublesome to most students when they are told that there is no thermal energy transferred, and thus no q to "plug in" to dq/T. Therefore, this is a useful teaching tool because students under slight stress are more receptive to learn the idea of measurement of entropy change by restoration of the system to its original state via a slow compression, the reversible inverse of the expansion. However, as detailed in Example 2, it should also be the occasion for emphasizing that entropy change is fundamentally an increase in the dispersion of energy and for introducing a molecular thermodynamic explanation for the increase in entropy with volume: a greater dispersion or spreading of the original, unchanged amount of energy within the system because there are more closely spaced microstates(7) in the new larger volume.
Entropy change in a number of other basic processes can be seen to be related to that in the expansion of a gas. The mixing of different ideal gases and of liquids fundamentally involves an expansion of each component in the phase involved. (This is sometimes called a configurational entropy change.) Of course the minor constituent is most markedly changed as its entropy increases because its energy is now more spread out or dispersed in the microstates of the considerably greater volume than its original state. (The "Gibbs Paradox" of zero entropy change when samples of the same ideal gas are mixed is no paradox at all in quantum mechanics where the numbers of microstates in a macrostate are enumerated, but will not be treated here.)
This is not the occasion for an extensive presentation of the use of energy dispersal in evaluating entropy change. These significant examples of the nature of entropy content of a substance and of the expansion of gases are indications of the utility of the concept in contrast to the verbalisms of order and disorder.
Disorderly molecules can be shown as scattered dots in an artist's drawing. This kind of clear picture can be equally clearly misleading in teaching the concept of entropy. Entropy change is an energy-dependent property. That is its essence. It cannot be grasped by an emphasis on the neatness of before and after snapshots of dots in space.
As discussed here in detail, disorder as
a description of entropy fails because it was needed (and therefore introduced
as an aid) in an era when the nature of molecules and their relation to energy
was just emerging. In the 21st century these relationships are relatively
well known. Disorder, a conceptual crutch for supporting a new idea in the
19th century, is now not only needless but harmful because it diverts students'
attention from the driving force that is the cause of spontaneous change
in chemistry, energy dispersal to(8) more microstates than were present in the
initial state. Disorder is too frequently fallible and misleading to beginners.
It should be abandoned in texts and replaced with a simple introduction to
entropy change as related to the dissipation of energy and to, at least, a
qualitative view of the relation of microstates to a system's macroscopic
state.(9)
I thank Ralph Baierlein (17) and Norman Craig for their invaluable aid and Brian Laird (14) and Walter T. Grandy, Jr. (11) for their support for this article. The suggestions of the reviewers were substantial and essential in improving the ms.