Entropy Sites — A Guide

June 2013

Dr. John M. Garland, M.D. and Ph. D. from Manchester University (U.K.), has informed me that his remarkable article -- an analysis of cancer that involves consideration of energy dispersal (entropy increase) and the spread of cancer to distant sites (in fractal terms) -- has been accepted by the Elsevier journal, "Critical Reviews in Oncology and Hematology" for publication in a couple of months.  We have communicated frequently over the past two years, but of course the content and its magnitude (51 pages of ms. with 155 references) are totally his accomplishment. (The abstract is at http://dx.doi.org/10.1016/j.critrevonc.2013.04.001.)

He summarized it for me thus:

This article arose from considering that the variety of different entities thought to induce cancer is huge, but that all cancer cells energetically behave identically; they become highly motile, proliferate seemingly without control, and their internal organisation becomes increasingly degenerate. So, if this energetic behavior is universal, why is there not a universal mechanism?

Until now, cancer induction is viewed/represented as from a deranged biochemical pathway, usually by mutation, whose components are arranged linearly and end in cancer-prone targets, for example DNA replication control or cytoskeletal activity. There are problems with this, for example: on the molecular scale, how different pathways intersect; how many are needed for a given effect; how all the myriad of biochemical pathways normally “fit together”; and progression and development of the universal phenotype. The first clue to cancer universality lies in the apparent switch  from regulated  structure and behavior to generalized increased dynamic activities at structural expense; as structure degenerates, dynamic activities such as motility and migration, replication and indeed clinical poor outcomes, increase.

Fundamental to all biochemical pathways is the constant flow of energy in chemical reactions. The interaction of that flow with the environment in which they  take place is crucial and inter-dependent. Thus, building cell structure or undertaking dynamic activity are always dependent on energy flow, the greater the energy available the more likely it is that a reaction will take place. However, in the process of structure-building the overall energy available for dispersal elsewhere becomes “locked in” while in dynamic activity it is constantly being dispersed or spread out. Cells normally co-ordinate these options through numerous checks and balances – always with the possibility of random distribution of energy in or out of the cell.  Thus, an unintended/unusual shift in cellular conditions could potentially favor dynamic activity that does not favor structure-building but rather random energy dispersal -- already suggesting a universal clue to cancer.

The interior of a cell is astronomically variable and for a cell to function the  environments managing all biochemical pathways must somehow be coherently organized. Nature widely uses a very simple tool, fractal geometry, to generate re-iterated “levels” of organization and which can deal with huge spatial variation. Clouds and snowflakes are examples. All different, but overall the same shape regardless of size. If we now apply fractal geometry to the distribution of energy flow in cells, they will self-assemble into fractal “corridors” where the components/reactions are decided by the amount of energy they dissipate or minimal energy states. This fractal “map” of energy dispersal is continuously changing according to energy demand, as in melting/freezing snowflakes, formation of clouds, generation of river patterns. The significance of this organization is that all parts are dynamically seamless; new areas can be added at different levels, and there are an infinite number of components that can fit into the same “space” (in the model termed Domains which at any level are absorbed into the next tier). The video files in the on-line article illustrate the creation of fractals which can be very easily conceived as energy flows arising from domains. However, and crucially for this model, every biochemical reaction is connected, in some way by its pattern of energy flow to every other. Further, pathways need not be linearly-ordered nor consecutive and components self-assemble according to ‘normal’ energetic criteria (see reference 155, Jun & Wright, Nat. Rev. Microbiol.8, 600, 2011). This provides the key to a universal framework both for normal cell operation and also for cancer; in cancer, the fractal network of energy dispersal is simply skewed towards maximizing that energy flow randomly in dissipation  rather than involving orderly structure and function.

The final element concerns the enormous unpredictable variability within cells; there are so many things going on at once. Chaos theory deals mathematically with unpredictability, and chaos can be linked to fractal geometry through descriptions of unpredictable behaviors which influence fractal formation. If this linkage is applied to fractal entropy, cell organisation is inherently stable overall because these variables effectively cancel each other. For cancer, however, the situation is different. Cancer-inducing agents all share the property of being permanently active (i.e. they uniformly favor the random dispersal of energy rather than its use in creating structure)  whether in a suppressive or activation mode. The effect of this is to replace variability with a constant dissipative component and permanent re-alignment of energy flow toward random dispersal.  Over time the network becomes increasingly focused on dissipation and activities with the highest abilities, i.e. dynamic activity, lead to the self-generating progressive disturbances recognized in cancer.

Many aspects of the model are amenable to testing, for example using mathematical modelling or exploring how enzyme systems energetically self-assemble in complex mixes.

[In the Acknowledgements section of Dr. Garland's article, he refers to "Professor F. Lambert (Occidental College, USA)" and then concludes with "This paper is dedicated to Professor Lambert for his work on the fundamental applications of entropy."]

November 2012

An ex-student has just referred me to an important article by two professors in a Japanese university, http://onlinelibrary.wiley.com/doi/10.1111/j.1749-6632.2009.05166.x/full#b9. It deals with the errors of many economics experts, from Georgescu-Roegen of 40 years ago up to the present, in their naïve attempts to connect economics to thermodynamics.  Paragraph 2.6 in that article - about my view of entropy in thermo - is a neat summary.

Josh Floyd (whose important article about misapplying entropy ‘everywhere’ is cited in the Archives of this website for April 2008 – just scroll down!) had previously castigated Georgescu-Roegen on Amazon.com (awarding his book with one star – only because Amazon doesn’t permit 0 stars!):  http://www.amazon.com/The-Entropy-Law-Economic-Process/product-reviews/1583486003/ref=cm_cr_dp_qt_hist_one?ie=UTF8&filterBy=addOneStar&showViewpoints=0

Floyd also evaluated Rifkin’s “Entropy Entropy Entropy” correctly in Amazon.com with Amazon’s one star (i.e., 0 stars!) in http://www.amazon.com/Entropy-A-New-World-View/product-reviews/0670297178/ref=cm_cr_dp_qt_hist_one?ie=UTF8&filterBy=addOneStar&showViewpoints=0

Most important:  I have just discovered Floyd’s thought-provoking ‘continuing’ web page “Beyond This Brief Anomaly”.  Its address is that:  http://beyondthisbriefanomaly.org/

October 2012

A statement about the importance of entropy as energy dispersal in a chemical reaction is in the sixth edition of Vollhardt and Schore’s “Organic Chemistry” text:

“If the enthalpy of a reaction depends strongly on changes in bond strength, what is the significance of ΔS°, the entropy change? You may be familiar with the concept that entropy is related to the order of a system: Increasing disorder correlates with an increase in the value of S°. However, the concept of “disorder” is not readily quantifiable and cannot be applied in a precise way to scientific situations. Instead, for chemical purposes, ΔS° is used to describe changes in energy dispersal. Thus, the value of S° increases with increasing dispersal of energy content among the constituents of a system. Because of the negative sign in front of the TΔS° term in the equation for ΔG°, a positive value for ΔS° makes a negative contribution to the free energy of the system. In other words, going from lesser to greater energy dispersal is thermodynamically favorable.

What is meant by energy dispersal in a chemical reaction? Consider a transformation in which the number of reacting molecules differs from the number of product molecules formed.  For example, upon strong heating, 1- pentene undergoes cleavage into ethene and propene. This process is endothermic, primarily because a C–C bond is lost. It would not occur, were it not for entropy. Thus, two molecules are made from one, and this is associated with a relatively large positive ΔS°. After bond cleavage, the energy content of the system is distributed over a greater number of particles. At high temperatures, the –TΔS° term in our expression for ΔG° overrides the unfavorable enthalpy, making this a feasible reaction.”

September 2012

Professor Leff has not only completed the publication of his five articles in the Physics Teacher mentioned below, but made them fully available online at http://www.csupomona.edu/~hsleff/selpubs.html.

Already, one author of a physics text has stated that he will use Leff's approach to entropy in it.

February 2012

Professor Leff’s articles

Please click the Archive section of this site for June 2008 for a full introduction:

Physicist Harvey S. Leff (Professor Emeritus of the California State Polytechnic University, Pomona)  published the first article that quantitatively presented the idea of entropy involving the dispersal or spreading of a system’s energy, with entropy as a measure of such spreading, in 1996  (Am. J. Phys. 1996, 64, 1261-1271).  When I learned about it in 1999, I inserted a Note to it in my “Entropy Is A Cracked Crutch” ms. (published in February 2002) and gave more proper credit as the lead reference in my next article, “Entropy Is Simple, Qualitatively” (October 2002),

Now Professor Leff has begun a series of five articles in the Physics Teacher. As might be expected, because they are intended for physicists, they will be far more rigorous mathematically and theoretically than my qualitative approach to entropy.  The first article appeared in the January 2012 issue: H. S. Leff, Phys. Teach., “Removing the Mystery of Entropy and Thermodynamics --- “Part I”, 50, 28-31 (2012); in February appeared “Part 2”, 50, 87-90 (2012). The subsequent Parts will be published monthly

Online article – why the concept of entropy was considered so difficult – and why it isn’t.

In October, the editors of an online scientific journal invited me to develop a guest editorial.  It is online at lambert2011.pdf. I chose what might appear to be an egregious title, "The Conceptual Meaning of Thermodynamic Entropy in the 21st Century", but it is not.  As stated in the last lines, a majority of the future leaders in US chemistry by mid-century will have been introduced to entropy via this concept of its being a measure of energy dispersal.

The initial goal of the brief article was to explain why brilliant physicists and chemists of the past century failed to explain entropy clearly - i.e., failed to develop an adequate conceptual explanation for the success of dS = dq/T. Certainly, the ‘driving force’ in this relationship is simple: the nature of q, energy.  A common property of energy is that all types – including molecular energy -- tend to spread out, disperse in space if constraints are lessened or removed. It was simply unfortunate that Boltzmann's "disorder" comments of 1898 became the dominant “meaning” of entropy for so long.

This journal reports the number of downloads of its articles on its index page.  Surprisingly, the number for this editorial exceeded 1300 by late February.  (It is a legitimate count !  I had suspicions that the Journal may have manipulated them, but a friend who can access such arcane matter sent me a list of 800 when I asked him.)

January 2012

As I mentioned  two years ago, a truly excellent text, the 2nd edition of Burdge’s “Chemistry” was published.  Now, with Dr. J. Overby, Burdge’s  text has been revised to present an ’atoms first’ approach for those who prefer it..
Both texts are unusually good in their depiction of entropy. Not only have all references to entropy as “disorder” been eliminated but, far beyond this, “what entropy is” is uniquely handled.

Featured throughout each text are 16 two-page “Visualizing Chemistry” (large drawings/illustrations) of important points, many extended to online animations available to student users.  That feature in the thermodynamics chapter depicts six examples of system change that are correlated with entropy change and ‘particles in a box’ energy levels – volume increase, temperature increase, molecular complexity change, molar mass, phase change, and chemical reaction.  Many good texts only attempt to show such differences via energy levels for volume expansion and temperature increase.  None supplement with animation as do Burdge or Burdge and Overby..

Further, I am impressed by the wide utility of the text for a large span of students’ competence – specifically re my focus on the presentation of entropy.  Due to information I have received from instructors in the classroom, almost all students readily accept the concept of entropy as measuring how widely spread in space or in additional particles, the energy of molecules (or that which is supplied to them) becomes. However, too many students of average ability ‘get stuck’ when microstates are introduced in any meaningful detail.

Burdge barely mentions the word, microstate – her ‘particle in a box’ energy levels are left at that, as greater spreading out of energy – volume increase, closer levels; temperature increase, more occupancy of higher levels, etc.  I think this is optimal, because it is clear over the whole span of  students’ abilities in gen chem.  (And, if desired, in a very short discussion only for students going on to physical chemistry, a basic relation of numbers of energy levels/microstates and entropy change can be elucidated.)

November 2011

An article about carbon nanotubes – tiny hollow tubes of carbon atoms (ca. 25 to 100 thousandth of the thicknessof a human hair) – whose properties of rapidly absorbing water were found to be related to entropy and enthalpy changes appeared in a recent issue of the Proceedings of the National Academy of Sciences.   (The complete article is available via http://www.pnas.org/content/108/29/11794)
The PNAS abstract below uses the words entropy and enthalpy in a traditional manner.  Following it, my expansion of the abstract in terms of viewing entropy as energy spreading out to the surroundings due to hydrogen bonds being broken when water molecules move into minute CNTs (and seeing that enthalpy increases in one particular CNT size because stronger hydrogen bonds are formed) – more clearly explains exactly what happens.

Entropy and the driving force for the filling of carbon nanotubes with water

Tod A. Pascal^a,^b,  William A. Goddard^a,^b,¹,  and Yousung Jung^a,¹ a Graduate School of Energy, Environment, Water, and Sustainability, Korea Advanced Institute of Science and Technology, Daejeon 305-701, Korea; and b Materials and Process Simulation Center, California Institute of Technology, Pasadena CA 91125 Contributed by William A. Goddard, May 25, 2011.

Abstract

My ‘translation’ of the above abstract of fundamental CNT research – in terms of entropy as a measure of energy spreading out in the surroundings in a process and enthalpy as energy becoming incorporated in stronger chemical bonds in a process:

Water spontaneously flows into extremely small carbon nanotubes (CNTs)   --  but why should it?  What is the ‘driving force’?  Carbon does not attract water!

Each molecule of ‘bulk’ or ordinary water (or ice) is about 0.3 nm (nanometers) in diameter and is strongly attracted to two other water molecules by 4 hydrogen bonds, HBs.

Two HBs are due to the H atoms of a particular water molecule being attracted to the (lone electron pairs) of another water molecule. Two additional HBs are formed between the lone pairs of that ‘particular’ water molecule, acting as acceptors in being attracted to the H atoms of a third water molecule. However, all water molecules are rapidly and ceaselessly breaking such bonds while instantly forming similar hydrogen bonds with other water molecules as they continually move in any body of water – whether a large tank, a beaker, or a thimble.

         Of course, there is no attraction between water molecules and the carbon walls of a CNT, so any water molecules within a CNT that are touching the walls cannot be attracted to them as they were previously hydrogen-bonded to adjacent water molecules.  Thus, each water molecule next to the CNT walls must lose one or two hydrogen bonds in entering the tube – and the amount of energy in that loss as similar water molecules enter must be spread out to the surroundings:  to the tube walls, to outside molecules.  Clearly, this process of greater energy dispersal in space compared to bulk water is favored – it is an increase in entropy.

         Because of the size restrictions inside the smallest CNTs, e.g., those with an 0.8 nm diameter, only about “two plus” water molecules per cross-section of the CNT, with three or fewer such “cross-sections” per nm of the CNT length is probable.  This means that the energy of some 12 hydrogen bonds in the water per nm of the length of the tube, must be dispersed from bulk water if/when it moves into such a CNT – a comparatively large spreading out of energy as/after water molecules enter, and thus a very favored process energetically:  the cause of spontaneous movement of water into 0.8 nm CNTs is an entropy increase.

         Also, because there are fewer H-bonds on each water molecule – i.e., considerably less attraction between each molecule in the chain/line/assembly of water molecules in the CNT than in “bulk water” – those water molecules in an 0.8 nm CNT are slightly freer to move than in bulk water, a little bit more like a gas than like a liquid (i.e., a “vapor-like phase” in the scientific abstract).

         Surprisingly, a slight difference in diameter causes quite different arrangements for the water molecules.  In 1.1-1.2 nm diameter CNTs, the water that enters and is ‘lined up’ the length of the tubes has enough space for more molecules per nm of tube length (but more hydrogen bonding between adjacent molecules than in 0.8 nm tubes).  Thus, their limited motion due to slightly more hydrogen bonding causes them to line up (“stack up”) less freely than in bulk water -- almost as though they were in an ice-like structure.  But such firmer bonding arrangements compared to bulk water is an enthalpy increase.  Again, although here aided by stronger bond formation rather than only HB breakage, movement of water molecules into a 1.2-1.2 nm diameter CNT is energetically preferred to their remaining in bulk water.

         In CNTs larger than 1.4 nm, relatively fewer molecules -- but still a very substantial number --  have some of their hydrogen bonds broken as they enter  >1.4 nm CNTs compared to smaller CNTs.  Therefore, despite a lesser quantity, this decrease in inter-molecular bonding results in the dispersal of some bond energy to the surroundings – i.e., an increase in entropy of the ‘universe’ of surroundings and system, when water molecules enter the larger CNTs. 

April 2011

I worked hundreds of hours on several sites in Wikipedia in 2006 and some in 2007. However, because no one can put their own bio in Wikipedia, it is quite an honor that an important Wikipedia administrator has installed my bio -- with the only recent picture that I have -- too much of a smile and all. Click on:  Wikipedia Frank L. Lambert.

July 2010

It was just reported to me that the Dean of a university wrote a blog item in 2009 about my ‘Gutenberg Method' of teaching referring way back to its being featured by the editor of the Journal of Chemical Education in 1963. JCE1963.pdf  Below is an excerpt, with corrections and citations added by me.

Robert T. Morrison, co-author of the leading organic chemistry text for some 30 years, died in April. (We were friends in our graduate school days at the University of Chicago.)  If you teach organic or have taken a course in it, you should read his lecture against lecturing (as mentioned by Dr. Eubanks, previously) — the funniest ever given seriously at a University of Chicago conference, or any other!

February 2010

The 2nd edition of Burdge’s Chemistry was published in late January.  It is truly excellent. Not only have all references in the previous edition to entropy as “disorder” been eliminated but, far beyond this, the introduction to “what entropy is” is superbly handled. Featured throughout the text are 16 two-page “Visualizing Chemistry” (large drawings/illustrations) of important points, almost all extended to online animations available to student users.  That feature in the thermodynamics chapter depicts seven examples of system change that are correlated with entropy change and ‘particles in a box’ energy levels – volume increase, temperature increase, greater mass of molecules, lesser or greater structural complexity (i.e., the latter with more energetic modes), etc.  Most good texts only attempt to show such differences via energy levels for volume expansion and temperature increase.  None supplement with animation.

Further, I am impressed by the wide utility of the text for a large span of students’ competence – specifically re my focus on the presentation of entropy.  Due to information I have received from instructors in the classroom, almost all students readily accept the concept of entropy as measuring how widely spread in space the energy of molecules becomes. However, too many of average ability ‘get stuck’ when microstates are introduced in any meaningful detail.

Burdge does not go into microstates at all – her ‘particle in a box’ energy levels are left at that, as greater spreading out of energy – volume increase, closer levels; temperature increase, more occupancy of higher levels, etc.  I think this is optimal, because it can become clear for all levels of ability in a class, especially with Burdge’s visual aids.  Then, an hour or two only with those students going on to physical chemistry (linking energy dispersal in space with the increased number of accessible microstates and the Boltzmann equation, plus the Boltzmann with Clausius’ entropy) is adequate preparation for chemistry majors’ later course.

January 2010

Entropy Re-mystified?

I have finally read a book that I was told had become popular, “Entropy Demystified”.  It is a 217-page disaster to anyone wanting to understand entropy and the second law.  Most of the lengthy evaluations that praise the book on Amazon.com seem to have been written by the author's best friends, several being mature physicists – rather than by persons trying to understand entropy for the first time.  The following is more objective than those "reviews":  giving it a rating of “no stars” out of a possible five.  (However, Amazon.com, for a reason you might guess J, increased that rating to “one star”.)

Fifty years ago, Arieh Ben-Naim, as every student in a physics or chemistry class of that era, was mystified by his introduction to entropy and the second law of thermodynamics.  Although he became a professor of chemistry at the University of Jerusalem before retiring 15 years ago, Ben-Naim has evidently not kept up with the teaching of those topics in current chemistry texts.  Thus, he seems unaware that most general chemistry texts currently published in the US (16) and three in physical chemistry now clearly and simply present entropy and the second law (Check “May 2009” in this website).

Therefore, his 217 pages of “Entropy Demystified” that are necessary to develop his personal viewpoint (an information theory variant, not present in any US undergraduate chemistry textbook) can be clarified by 3-4 pages in each of the chemistry texts listed in this site at “May 2009” with their ISBN numbers.

In fact, a conceptual summary of the second law and entropy for all chemistry students and many non-scientists can be abstracted from these texts in two sentences:  “Energy of all types in chemistry changes – if it is not hindered – from being localized in one volume to becoming more dispersed, spread out, distributed in space (and abstractly at one instant, in any one of many more energy quantum states, microstates, than were accessible before the change).”  Then, “entropy change is the quantitative measure of how much more widely distributed the initial energy becomes in a spontaneous process in chemistry.”  Thus, in real processes, energy literally spreads out in space, and abstractly, at each instant, is in one microstate of a maximally probable number of quantum states (microstates) that are consistent with a final macrostate at equilibrium.

Unfortunately, Professor Ben-Naim’s fundamental error, summarized on page 204 but vitiating all previous pages, is his misinterpretation of what happens in real systems of molecules, especially in the simple isothermal expansion of ideal gases or in their mixing or expansion.  These cases have misled him to focus on the lack of change in the total energy of the system, rather than on what is actually the fundamental cause of all thermodynamic entropy change in chemistry:  the increased spreading of the initial energy of actual molecules in space when constraints are removed – e.g., their spontaneously moving into a greater volume from a smaller volume (with unchanged energy) in a process such as expansion or mixing.  This is what traditional thermodynamic entropy readily measures and, as just stated, can be readily understood.

Ben Naim admits, in italics, the disconnect between information and the second law on page 203 of “Entropy Demystified” by writing “a measure of information cannot be used to explain the Second Law of Thermodynamics.”  This is true, indeed. The connection between the second law and information is tenuous. 

Contrast this with the modern view in beginning collegiate chemistry texts, e.g. “whenever a product-favored chemical or physical process occurs, energy becomes more dispersed...This is summarized in the second law of thermodynamics, which states that the total entropy of the universe ... is continually increasing.” (Moore, Stanitski, and Jurs; 3rd edition.)  A popular physical chemistry text that is used world-wide states “...the Second Law of thermodynamics, may also be expressed in terms of another state function, the entropy, S. ...entropy...is a measure of the energy dispersed in a process...” (Atkins and de Paula, 8th edition.)

The connection between the second law, spontaneous chemical reactions or physical processes, dispersal of energy, and entropy is integral, tight, and widely accepted in chemistry books.  It does not require 200 pages for its justification.

August 2009

In “what’s new” for August 2007 I described my article that showed how texts that introduced ‘positional’ (configurational) entropy to students would totally mislead them:  beginners are taught that “matter tends to become dispersed” and that there are two “types” of entropy rather than one.  Equally disastrous to students’ understanding is a focus on the ‘probability’ of molecules’ positions as the sole factor in entropy increase.

[Entropy increase is first enabled by molecular motional energy (rapidly moving or vibrating molecules); only then is entropy increase actualized by the probability of a maximal dispersal/distribution of that energy – in space, within each microstate of a greater number of accessible microstates.]

A far more fundamental article by Professor E. I. Kozliak has just been published in the September issue of the Journal of Chemical Education, “Overcoming Misconceptions about Configurational Entropy in Condensed Phases”.   (He had previously resolved the old problem of incorrectly understanding “residual entropy” as simply due to molecules’ locations in space.)

May 2009

A minority of US general chemistry texts for majors still describe entropy in terms of “disorder” – an unfortunate subjective concept whose source appears to be a naïve statement by Boltzmann (boltzmann.html).  Now, however, most  ‘gen chem’ texts have discarded this non-scientific view and describe both entropy (e.g. standard molar entropy) and entropy change as measuring the result of energy becoming dispersed in physical or chemical processes – literally spreading more widely in space, while abstractly dispersing on additional energy levels in a conventional “particle in a box” diagram of one microstate.  (The latter, of course, then directly implies a greater number of microstates, W, in any final macrostate.)

It was eight years ago that the ms. outlining the above approach was accepted for publication (that now, revised and corrected, is available at this site: entropy_is_simple.

April 2009

There have been some noteworthy improvements in texts’ treatment of entropy in terms of energy dispersal.  A few will be mentioned here.  In May will be listed the 21 chemistry texts that no longer define entropy as “disorder” but rather emphasize molecular energy dispersal, concretely in space or abstractly on more energy levels in each microstate, as a useful approach to understanding standard entropy and entropy change.

Physical Chemistry

• Levine, in his new 6th edition of “Physical Chemistry”, well develops entropy, S, as a measure of the probability of a thermodynamic state.  On page 101, he states “…order and disorder are subjective concepts, whereas probability is a quantitative concept.  It is therefore preferable to relate S to probability rather than to disorder.”   Then, he summarizes,  “…it is the distribution of energy (which is related to entropy) that determines the direction of spontaneity.”

  The final sentence of the preceding section is “The website entropysite.com contains several articles criticizing the increasing-disorder interpretation of entropy increase and promoting the increasing-dispersal-of-energy interpretation.”  

  To be cited by Levine is indeed an honor.

General Chemistry

• McMurry and Fay have completely discarded “disorder” from the 5th edition of their text.  However, they emphasize randomness as the key to understanding entropy rather than a start to that goal:  It is energy that is being carried by randomly moving molecules as far as they are allowed to move that results in a probable energy distribution, a final equilibrium state.

• Chang, in his 10th edition of “Chemistry” has also eliminated any mention of “disorder” in connection with entropy in this most recent of a distinguished series.

• Kotz, Treichel and Townsend in their 7th edition have markedly improved their previous introduction of spontaneity and entropy, with an even more clear and complete exposition.  They surpass several authors who still separate the dispersal of energy from the dispersal of molecules.  Matter, in chemistry, never spreads out without the intervention of energy (macro matter), unless it is a carrier of energy (molecular matter above 0K).

General Chemistry for non-majors

• Hill, Kolb, and McCreary in their 12th edition of “Chemistry for Changing Times” have now adopted their introduction of entropy as “a measure of the dispersal of energy in a system…” with no reference whatsoever to ‘disorder’.

  
  

March 2009

• Unfortunately, I had not seen a copy or excerpts from the 2008 2nd edition of Gilbert, Kirss, Foster and Davies “Chemistry: The Science in Context” until last week. The authors have remarkably improved their treatment of thermodynamics in this edition. Not only have they completely eliminated any mention of “disorder” in connection with entropy, but their presentation of spontaneous processes and entropy is unusually well done.
  
  Admittedly from anecdotal evidence, but not only from my geographical area, I am becoming convinced that the majority of students in general chemistry classes are ‘overtaught’ about microstates. In contrast to those texts emphasizing ‘positional entropy’ and spending an inordinate amount of time and space on probability to introduce microstates, Gilbert and his collaborators directly present energy levels and simple statements about arrangements on energy levels as their four-paragraph intro to the Boltzmann equation. This is characteristic of their entire thermo chapter — well-presented and sufficient — but not too much.

 

January 2009

• A standard molar entropy, S⁰, is the absolute (i.e., not ‘relative’) measure of the entropy of a substance at 298.15 K.  It is extremely important because these S⁰ values are essential for so many areas of chemistry and chemical engineering to predict the outcome of reactions via the Gibbs equation, its most simple form being  ∆G⁰ = ∆H⁰_formation - T∆S⁰.

  The January 2009 issue of the Journal of Chemical Education contains an unusually important article by physics professor Harvey S. Leff and me — important because it shows a surprisingly simple linear correlation.  The S⁰ of 77 solid substances, widely differing in type  —  e.g.,from Cu to NaCl to UF₄ to C₂₀H₄₂ —  and the quantity of enthalpy, ∆H⁰, added to them while they were heated from 0 K to 298.15 K are closely linked.
  
  The equation is:  S⁰ = 0.0066  ∆H⁰ /K    Notably, ∆H⁰  ≈ U⁰, the internal energy stored at 298.15 K.    (The deviations of “outliers” from the 0.0066 line are readily explained in the Supplement.)
  
  
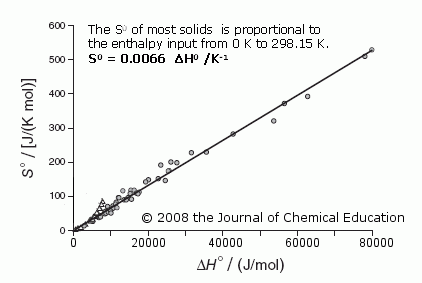
  There is no “mystery” to entropy here, no place for old subjective terms like “disorder”, or such new terms as “missing information” ! Entropy in this most fundamental case is simply a measure of the spreading of energy within a cooler substance from its warmer surroundings when it is heated —  starting with the cooler substance near 0 K and summed up, degree by degree, to 298.15  K, the ‘standard’ temperature.
   
  The amount of spreading/energy dispersal depends upon the material in which the spreading occurs and the amount of energy added to it.

  This is indeed a nice corroboration of what I wrote in 2002, “The entropy of a substance at any temperature T is not complex or mysterious.  It is simply a measure of the total quantity of energy that had to be dispersed within the substance from 0 K to T so the substance could exist as a solid or liquid or gas at the designated temperature.”

   

November 2008

• A fundamental article about “residual entropy” by Professor E. I. Kozliak and me is now available here.  Residual entropy, the entropy remaining in crystals of some compounds even near absolute zero, e.g. CO, N₂O and H₂O, has traditionally been accounted for (and counted) just from the number of different molecular arrangements in the crystal. From this, chemists have felt that entropy can depend only on a “position in space”, regardless of a substance’s internal energy.  Unfortunately, residual entropy has been the ‘poster boy’ of an example of “positional entropy”.
  
  In a previous article, Kozliak showed that the results from counting procedures in residual entropy calculations are identical to those from considering the different forms on different energy levels — a novel focus on entropy values as related to energy distributions in substances like CO, rather than on the  number of arrangements of the molecules, their  “positions in space”.
  
  In this 2008 article, Kozliak shows how residual entropy is inherently coupled to the corresponding latent heat which would be released upon cooling if a reversible path were available.  That such a process is not fanciful for CO or N2O (although not yet achieved) is illustrated by the actual release of energy at very low temperatures by ice, when a small amount of KOH is added as a ‘catalyst’ and ice XI is formed that has no residual entropy.

August 2008

• In the January 2008 Journal of Chemical Education Dr. Frank B. Ellis and David C. Ellis published details of the construction and applications of a shaking apparatus with chambers in which beads can be used to analogize the behavior of molecules.  They described its versatility in demonstrating/analogizing 'molecular behavior' in equilibrium, bond energy, endothermic reactions and other areas, including entropy.  In describing entropy, they referred to an older text that stated "entropy is disorder".  However, when I wrote them about most modern texts having changed to say that entropy increase should be viewed as an increased spreading out of molecular energy, they agreed to a Letter to the Journal which corrected the obsolete statement about entropy. The Letter appeared in the just-published September issue of the Journal.

July 2008

• For the 20th Biennial Conference on Chemical Education held in July on the Indiana University campus, one of the symposiums was organized by Dr. Barbara Murray of the University of Redlands with the theme of "Engaging Students in Organic Chemistry".  There were a number of speakers and in her symposium Dr. Murray was kind to distribute copies of the following:
  
  The funniest lecture about chemical education (that could have been titled "Why Do Chemistry Profs Still Lecture, Since Gutenberg Made Printed Textbooks Possible?") was given by Professor Robert T. Morrison, co-author of the famous organic chem text, Morrison and Boyd.  We all know about the book that changed O-chem texts forever.  However, few instructors have ever heard of Morrison's 1986 lecture at the U of Chicago that applies to all beginning classes in chemistry, and perhaps even to physical chem.
  
  
• Details of my 'discovery' and the most effective implementation of the 'Gutenberg Method' are here.

June 2008

• I failed to announce a most important publication about entropy, “Entropy, Its Language, and Interpretation”.  It was written by Professor Emeritus of Physics Harvey S. Leff (of the California State Polytechnic University, Pomona) and appeared in Foundations of Physics, 2007, 37 (12), 1744-1766.  The abstract is available here and, of course, the full article is in the journal or online through one’s institutional library.

  As indicated by its length and the eminence of the journal, this article is both thorough and theoretically sound in presenting the increase in entropy as fundamentally a spreading of energy spatially during processes and its greater temporal spreading over accessible microstates after such an entropy increase.

  “Temporal spreading” means that a system’s total energy (e.g., that of an ideal gas) in a single microstate at one instant in time — a particular arrangement of its molecular energies on quantized energy levels —  will change, in the next instant of time, to a different arrangement/microstate.  Then, if after a process there is a greater number of accessible microstates than before, a few or many different microstates are more likely to be reached from an initial microstate in a second of time or so over which a measurement is made.  It can be seen that this is a “greater temporal spreading of the system's energy” in the sense of a “temporal dance” over the same number but probably a few or many more different microstates than prior to the process. 
            The notion of temporal speading that increases with the number of accessible microstates (W) is consistent with, and provides a new interpretation for the Boltzmann entropy, S = k_B ln W, where k_B is Boltzmann’s constant.
            It is appropriate to see entropy’s symbol S as shorthand for spreading, a coincidental memory aid for beginning students.

  Professor Leff published the first article that quantitatively presented the idea of entropy involving the dispersal or spreading of a system’s energy, with entropy as a measure of such spreading, in 1996 (Am. J. Phys. 1996, 64, 1261-1271).  I inserted a Note to it in my “entropy is a cracked crutch” ms. in 2001 while giving more proper credit as the lead reference in my next article, “Entropy is Simple, Qualitatively”.   When the focus is on energy spreading out — or dispersing as I happened to choose before reading his article, entropy can indeed be seen correctly as being relatively simple:  It is a passive measure/’meter stick’ both of how much energy has spread (and how it has spread, i.e., at what heat capacity and at what temperature(s)) and how widely in space it has spread out (in isothermal processes such as gas expansion or in mixing).

  I am indebted to Professor Leff for aid over the past six years.  We have just collaborated on a very important article (to be published within the next five months) that should convince the last doubters of the value of our viewpoint.

April 2008

• Joshua Floyd, with a background in engineering and now teaching at the Australian Graduate School of Entrepreneurship in the Swinburne University of Technology, Victoria, Australia, has published a brilliant and scholarly article, "Thermodynamics, entropy and disorder in futures studies". Its abstract is below. (The article is accessible via college or university library e-journal services.) He discusses the manifold misuse of the second law of thermodynamics over many years and by many economists, IT specialists, serious professionals involved in futures studies, and not-as-serious popularizers. The major error in most of their writing is an assumption that this law, derived from studies of the energetic behavior of atoms and molecules, applies to “order or disorder” in the material objects with which we all must deal

  Futures  39 (2007) 1029-1044. Abstract

  The conceptual bases of futures studies are constrained by physical reality only to the extent that we construct these according to our best understanding of physical principles. This places a burden on futures practitioners to ensure that engagement and use of these principles is sufficiently robust to protect the plausibility of their work. The second law of thermodynamics is widely recognized as having fundamental implications for the nature of our physical reality. It is also widely misinterpreted, leading to distorted understanding of this reality. Thermodynamic principles are frequently referred to in the futures literature, and are sometimes fundamental to the futures thinking underlying the work. Reflecting the widespread misunderstanding of the second law, usage in the futures literature is usually problematic. This has implications for the value of the work, and also for the credibility of the field. In this article, the problem is demonstrated, and an updated interpretation of the second law is introduced. The origin of the problem is examined from historical and scientific perspectives within the thermodynamics field. The updated interpretation's implications are examined in the context of futures and other transdisciplinary perspectives.

  Article Outline

  1. Introduction: thermodynamics in futures studies
  2. An introduction to the problem, and to a response
  3. Understanding the problem: some history and science of thermodynamics
  4. Reinterpreting the second law: the futures studies context
  5. Conclusion
  References

   

October 2007

• In his new book “Notes From the Holocene (A Brief History of the Future), Dorion Sagan, science author and eldest son of the late Carl Sagan, writes:

  “Publications in the Journal of Chemical Education by Occidental College professor emeritus Frank L. Lambert have drawn attention to the century-old non-scientific mantra, entropy-as-disorder, altering the modern textbook landscape.  [By April 2007, authors of eighteen chemistry textbooks] had deleted their previous identification of entropy as “disorder”.  The new texts describe the second law as being fundamentally a matter of energy dispersal.  If energy is not hindered, it spreads out.”

  Invited to speak as a registrant at the International Thermodynamics Symposium at MIT on October 4-5,  Sagan opened his remarks in the Session, “Foundations of the Second Law”, with the above quotation from his book.

August 2007

• The September issue of the Journal of Chemical Education has my article which shows why the statement in some texts (e.g., those numbered 11-13 in December 2005) that "Matter tends to become dispersed" is seriously misleading, It is a misinterpretation of a result from configurational (positional) entropy — itself a viewpoint that should not be introduced to general chemistry students because they then believe that there are two "types" of entropy rather than one. The article concludes with the important statement, "Two factors are necessary for entropy change in chemistry. An increase in thermodynamic entropy is enabled in a process by the motional energy of molecules (that, in chemical reactions, can arise from the energy released from a bond energy change). However, entropy increase is only actualized if the process results in a larger number of arrangements for the system's energy, that is, a final state that involves the most probable distribution for that energy under the new constraints"

June 2007

• In the July issue of the Journal of Chemical Education, Dr. M Sözbilir reports the results of an unusually detailed survey of individual Turkish undergraduates’ understanding of entropy. Not only had all the students taken a first course in chemistry, but all of them in these physical chemistry classes were being trained to be chemistry teachers. However, the basic conceptual model in both of those courses was that an increase in thermodynamic entropy is related to an increase in disorder.  Thus, it is hardly surprising that  “[s]tudents’ understanding of the basic aspects of [entropy] are—in many cases–limited, distorted or wrong.”  Dr. Sözbilir’s findings are supported by his references to similar conclusions from Scotland, South Africa, and Portugal.  Clearly, students everywhere need modern texts that present the concept of entropy as a measure of the dispersal of energy within a system or between the system and its surroundings!  (See the 1898 origin of the confusing idea of ‘disorder’ being associated with entropy here.)                       

April 2007

• In addition to the 16 chemistry textbooks described in March 2006 and December 2005, two more texts now introduce entropy in terms of energy dispersal within a system or in the universe of a system plus its surroundings.

  17. A thorough new general chemistry text by Tro (Prentice-Hall, 2008) introduces the concept of entropy early in his presentation of solutions.  He describes the mixing of two gases, initially separated, as due to the kinetic energy of each kind of molecule becoming more spread out in the final larger volume. Immediately, he mentions the parallel of the thermal energy in one end of an iron bar inevitably becoming dispersed throughout the bar. In his later thermodynamic chapter, he mentions the possibility of considering the criterion for spontaneous chemical change as involving “disorder”.  However, in the next sentence he discards that possibility by defining and consistently using “Entropy (S) is a thermodynamic function that increases with the number of energetically equivalent ways to arrange the components of a system to achieve a particular state.”
  18. In the 7th edition of “General Chemistry” by Whitten, Davis, Peck, and Stanley (8th edition, Brooks/Cole, 2007) entropy change was described only in terms of “disorder”. I have not seen the new edition, but the publisher states, “The discussion of entropy in Chapter 15 has been expanded to include not only molecular disorder but also the concept of energy dispersal.”  In my admittedly biased opinion, that is a bit like saying “the reactions with oxygen and a metal have been expanded to include not only phlogiston but the formation of metal oxides with the evolution of heat.”  Nevertheless, it is indeed a step forward in describing entropy scientifically.

• The new 9th edition of “General Chemistry” (Prentice-Hall, 2007) by Petrucci, Harwood, and Herring continues the superb compact presentation of the previous edition, “…the way in which the energy of a system is distributed among the available microscopic energy levels is called entropy,” is immediately followed by the Boltzmann entropy equation, its relation to numbers of energy levels, and unusually clear depictions of levels in different ‘boxes’ and in a heated system.

March 2007

• " 'Disorder' in Thermodynamic Entropy", the historical origin of the introduction of 'disorder' by Boltzsmann, is now available here in response to many questioners.  The brief article also is an introduction for instructors who are not familiar with my approach to understanding entropy change. It closes with a description of the clear distinction between thermodynamic entropy and Shannon information "entropy".
  
  
• Professor E. I. Kozliak has published a noteworthy article in the March issue of the Journal of Chemical Education in which he resolved the old problem of understanding "residual entropy" , the entropy remaining in crystals of compounds such as CO, N₂O, FClO₃ and H₂O even as they approach absolute zero.  The entropy present in two or more arrangements of molecules in such crystals had only been considered in terms of "configurational" or "positional" entropy. Kozliak shows that the counting procedures in these entropy calculations are identical to what would result from considering the different forms on different energy levels -- a considerably more fundamental focus on entropy values as related to energy distributions.

November 2006

• A rather remarkable article by Arnd Jungermann, a secondary school educator in Germany, is in the November issue of the Journal of Chemical Education. For a number of years, he has treated entropy as a physical property that measures the amount of energy stored in a substance. His use of simple shelves and calculation of the occupancy of energy levels by a few particles, leads students to the conclusion that entropy is a measure of the occupied (accessible) energy levels. Then, development of atomic entropy values from S/R, shows relations of entropy to trends in the periodic table. "The way in which a material stores supplied heat or work is characteristic of its internal structure and is reflected in its molar entropy value."

June 2006

• My two sections, "The Second Law" and "Entropy", for the thermodynamics chapter of the Wikibook "General Chemistry" have just been completed. Click on the titles to reach copies that are here in the Supplements.  Although both contain material that is scattered on this entropysite, it is presented in somewhat different format, designed to be readily readable by beginners in chemistry and accessible by students not majoring in science.
  
  
• The new "Physical Chemistry" (Benjamin Cummings 2006) by Engel and Reid, both of the University of Washington, wisely omits any mention of the word 'disorder' in its exemplary definition of entropy on a phys chem level: "Entropy serves as a measure of the number of quantum states accessible to a macroscopyic system at a given energy."

March 2006

• Atkins' "Physical Chemistry" has been the best selling text worldwide in this subject for many years.  The new 8th edition was published in the US March 16. However, in previous editions Atkins described systems and entropy change in terms of order and disorder or chaos.  Even though he long has used the phrase, "the dispersal of energy", it was confined to an order-disorder view of thermodynamics — for example, to spontaneous changes being "always accompanied by a dispersal of energy into a more disordered state".   (Or "to chaos" in his book "The Second Law".)

  In contrast to the Second Law chapter of the 7th edition, which had some 27 instances of using "order to disorder" as a rationale for change, "disorder" and "disorderly" are mentioned only 3 times in the new 8th edition.  Atkins, with co-author dePaula, now state that their view of entropy "summarized by the Boltzmann formula is consistent with our previous statement [earlier in the chapter, re the dispersal of energy in classical thermodynamics] that the entropy is related to the dispersal of energy.

January 2006

• In 2005, the five sites about the second law and entropy change (see Links section) had a total of over 510,000 visitors and more than two million "hits".


• secondlaw.com is now ranked #1 in the Google list of over 10 million sources under the search term thermodynamics, as well as being ranked #1 out of some 1,500,000 results in a Google search of "second law". (That it is also #1 out of an astonishing 201,000,000 results from a search for second law without quotes is less noteworthy for secondlaw.com than for the apparent speed of Google in finding so many citations with both "second" and "law" in them!)


• 2ndlaw.com is ranked #1 in some 9,000,000 Google results for entropy.

December 2005

First-year college chemistry textbooks since about 1960 have used the 1898 description of thermodynamic entropy as “disorder”. In the February 2002 issue of the Journal of Chemical Education I showed that treating entropy change as “disorder” was not based on modern science and could mislead students. In the October 2002 Journal I urged that entropy be presented as the quantity of dispersal of energy/T or by the change in the number of microstates.

Textbooks do not alter their presentation of basic concepts readily nor rapidly. Thus, for the following 15 texts to delete “entropy is disorder” from their new editions within three years of my calling for such a drastic change is perhaps without precedent. Further, for all of them now to describe the meaning of entropy in various terms of the spreading or dispersing of energy (in some, quantified by Boltzmann's number of microstates) shows the utility of this concept in good teaching.

Textbooks for science majors

1. Moore, Stanitski, and Jurs' "Chemistry: The Molecular Science", whose first edition was the best-selling new text in a decade, has a 2005 2^nd edition (Thomson). The authors state that the new edition is improved because, among other features, the "...treatment of entropy in Chapters 14 and 18 has been rewritten to make it clear that entropy measures dispersal of energy" rather than "disorder". This text most thoroughly and most extensively applies my concept of "follow the energy flow" in aiding students to understand the concept of entropy.
   
2. Silberberg, in the 2006 4^th edition (McGraw-Hill) of his #1 or #2 best-selling "Chemistry" writes, "[The thermodynamics chapter] has been completely rewritten to reflect a new approach to the coverage of entropy. The vague notion of "disorder". has been replaced with the idea that entropy is related to the dispersal of a system's energy." and acknowledges my advice.
   
3. The 3^rd edition (Wiley, 2000) of Brady & Senese's "Chemistry" for science majors used "disorder"/order 65 times to describe entropy. However, in the 2005 4^th edition Senese told me that "disorder" is entirely omitted. In featuring their improvements for this edition, the authors state "We have changed our approach to presenting Thermodynamics... [by explaining] entropy as a measure of the number of equivalent ways to spread energy through a system."
   
4. Oxtoby, Gillis and Nachtrieb's 5^th edition of "Principles of Modern Chemistry" (Brooks/Cole) has removed any references to entropy as a measure of "disorder" that appeared in the 4 th edition. This text's relating of entropy increase to greater numbers of microstates as shown by the Boltzmann entropy equation is perhaps the most thorough in any general chemistry text.
   
5. Petrucci, Harwood and Herring in the 8^th edition of "General Chemistry: Principles and Modern Applications" (Prentice-Hall) have an unusually readable development of entropy as increasing when there are more microstates among which the energy of a system can be distributed. This is accompanied by a simple introduction to increased density of energy levels (and therefrom, more microstates) when the volume of a gas spontaneously increases.
   
6. The 2005 4^th edition of Hill, Petrucci, McCreary and Perry's "General Chemistry" (Prentice-Hall) still employs the word "disorder" in referring to entropy change in several places, but it is primarily as a bridge for those students who have heard the expression. Overall, the authors use my approach to entropy change as a dispersal of energy.
   
7. The 2005 8^th edition of Ebbing and Gammon's "General Chemistry" (Houghton Mifflin) includes some references to "disorder" in their treatment of entropy, but they emphasize that, fundamentally and scientifically, entropy involves energy dispersal as a function of temperature.
   
8. Ebbing, Gammon, and Ragsdale's 2006 (Houghton-Mifflin) "Essentials of General Chemistry" (785 pages rather than the 1200 in Ebbing and Gammon) has a similar treatment of entropy to the larger text, an emphasis on energy dispersal as essential to understanding entropy change.
9. Moog, Spencer and Farrell (Houghton Mifflin) have developed three paperbacks as a novel “Guided Inquiry” technique in areas of physical chemistry. Their 2004 “Thermodynamics” completely omits the references to “disorder” of “messy desks” in a previous trial edition and replaces them with viewing entropy as related to how energy can be spread out in a system.
10. A new text, “Physical Chemistry for the Life Sciences” by Atkins and de Paula (Freeman, 2006) omits the definition of entropy as disorder that was present in Atkins’ previous general chemistry and physical chemistry textbooks. Repeatedly, the emphasis in describing entropy change is on the dispersal of energy in the process. However**
11. The novel approach by Bell and his ten collaborators uses simple experiments or thought-experiments of “Investigate This” in developing concepts in “Chemistry: A General Chemistry Project of the American Chemical Society” (Freeman, 2005). Disorder is ignored as a definition or code word for entropy. Rather the student is led to consider arrangements of molecular energy in developing the Boltzmann relation. However**
12. The new 6th edition of “Chemistry and Chemical Reactivity” by Kotz, Treichel and Weaver (Brooks/Cole, 2006) have deleted their description of entropy increase as disorder that was in previous editions. They state that “spontaneous change results in dispersal of energy”. However**
13. Although previous editions of Olmsted and Williams “Chemistry” had 89 uses of “disorder” vs. “order”, including the definition of entropy, the 2006 4th edition (Wiley) defines entropy only in terms of energy dispersal. The word “disorder” is rigorously avoided in any context. However**
    
    **However, the preceding four texts each have the unfortunate concept of “the dispersal of matter” as though there were no motional energy considerations associated with such dispersal (as in gas expansion, or any type of mixing wherein the initial motional energy of the molecules becomes more widely dispersed in space). One even states that “Things tend to become dispersed.” The source of this error is dealt with here.
    
14. Brown, LeMay and Bursten's 2003 9^th edition (Prentice Hall) defined entropy only as "disorder". In a preliminary ms. of the thermodynamics chapter in their 2006 10^th edition all references to "disorder" were eliminated by one of the authors and the concept of energy dispersing or 'spreading out' more for increased entropy was used throughout. Although the published 10 th edition presents energy dispersal as a view of entropy, it includes the "extent of randomness" as equal, later stating “Each of these descriptions [of entropy] (randomness, disorder, and energy dispersal) is conceptually helpful if applied correctly.” This ‘trifecta' is an insurmountable challenge to beginning students who are readily confused even by a singular presentation of the concept.
    

Textbooks for non-science majors

15. The first edition of Suchocki's "Conceptual Chemistry" (Benjamin Cummings) introduced the second law as "Order Tends to Disorder". His 2^nd edition (2004) does so as "Entropy Is a Measure of Dispersed Energy"..."This fits with our everyday experience...." Then, with ΔS^o_React, Suchocki can lead even this group of students to understand the direction of chemical reactions.

August 2005

• The 2002 article in the Journal of Chemical Education, "Entropy Is Simple, Qualitatively" has been completely rewritten and expanded to amplify points that were novel at that time and to correct errors. The section describing microstates has new Figures and a far more detailed explanation.

July 2005

• The just-published book from the University of Chicago Press, "Into The Cool" by Dr. Eric Schneider and Dorion Sagan, has a subtitle that describes its theme: "Energy Flow, Thermodynamics, and Life". Emphasizing what lies behind the second law, energy's inevitable tendency to change from being concentrated in one place to becoming spread out [not just in space], Schneider and Sagan show that energy-gradients are vital to life. "[L]ife's increase in evolutionary complexity ...makes sense when we consider life along with other natural systems of energy flow." In describing how activation energies in chemical kinetics delay and obstruct energy flow and act as protective barriers to immediate second law action, the authors use my "Chemical kinetics firmly restrains time's arrow in the taut bow of thermodynamics for milliseconds to millennia" that corrects Eddington's overly simplified 1925 aphorism "The second law of thermodynamics is time's arrow ".

November 2004

• The November issue of the Journal of Chemical Education has two important articles using the “energy dispersal” approach to understanding entropy and one that is pertinent to the RT ln Q entropy function in the Gibbs free energy equation. (Also, in this issue is the formal letter to the editor that dealt with the article discussed in the “news” for April 2003). The article that upgrades the qualitative approach to entropy of this site to its quantitative application in physical chemistry by Professor E. Kozliak (University of North Dakota) is especially noteworthy.

October 2004

• For instructors in general chemistry, a detailed description of the dispersal of energy as fundamental in understanding the cause of entropy change — from gas expansion to chemical reactions — has just been completed. See "supplemental material" below.

March 2004

• At the National Meeting of the American Chemical Society, publishers exhibited new editions of their first-year college textbooks. The majority of them had discarded the definition "entropy is disorder" that was in previous editions and replaced it with a statement involving entropy as a measure of the dispersal of energy/T.
  

2003

Articles

• In the November JChemEduc, pp. 1271-74, Professor Robert Hanson (St. Olaf, MN) reports on “modeling” the equilibrium constant in a (catalyst-aided) isotope exchange equilibrium of H₂ + D₂ <-> 2HD with playing cards. He well develops concepts and details of the mathematical relation of probability to an equilibrium constant. However, as shown in “Shuffled Cards…” (Article 1 on this Web site), using playing cards to analogize chemical behavior can be misleading. Students and professors in the past often have not realized that cards cannot analogize the energetic movement of molecules (that leads to chemical equilibrium, or other results measured by entropy change) unless the cards also are constantly moving. In other words, only when cards are being vigorously shuffled do they become analogs of energetically colliding molecules. In a personal email, Professor Hanson expressed it concisely : “the shuffling [illustrates] the equilibrium, and counting [the probabilities from the card arrangements] is only taking snapshots.” I believed that his otherwise excellent article would be misunderstood by many readers because it may seem to them that chemical equilibrium is based on probability. However, probability only measures the results (“is a snapshot”) of the maximal spreading out of the energy of ceaselessly moving molecules. Card shuffling is enabling in   the analogy involving the probability of molecular equilibrium described in the article.