Entropy and the second law of thermodynamics

Student: Why the fast start? You took about 11 pages to get to entropy in that secondlaw.com/six.html. How come you're putting it right up front here?

Prof: Some readers e-mailed me that "What is entropy?" was the only thing they were interested in. For that introductory Web page, I thought some practical examples like forest fires and rusting iron (or breaking surfboards - and bones) would be a great introduction to the second law before talking about how it's all measured by "entropy". Wasn't that gradual approach OK?

S: Yeh. I think I understand everything pretty well, but I didn't want to take time to read any more in that secondlaw site after what you called page six. What's new about entropy that you're going to talk about here that wasn't back there?

P: [[Just a sidenote to you who are reading this: Sometime, click on secondlaw.com/ten.html, i.e., the "Last Page" of secondlaw site . It's based on chemistry, but it's not textbook stuff. It could profoundlychange your attitude about life -- and the troubles that will hit you sooner or later.]] Now, back to entropy. Remember some people are logging on to this site without having read secondlaw site. To bring them up to speed -- if you say you understood it pretty well, tell me about it as though I were a student.

S: Ha! You mean I can be up in front of the room with the chalk and you'll sit down?

P: Absolutely. Start from "What is the second law?" Then, go on to "What is entropy, really?" Those are the questions I'm always getting. Summarize your answers fast, maybe with a few simple examples, so new students can catch up and we all can go further.

S: OK, here goes..Rocks and balls fall if you drop them, tires blow out if there's a hole in them, hot pans cool down in cool rooms, iron rusts spontaneously in air, paper and wood in air will burn and make carbon dioxide and water (if you give them a little boost over their activation energy barrier secondlaw.com/three.html ) You think these are all completely different? Sure, they are, but they're all due to the same cause -- some kind of energy in them spreads out!

Whether it's rocks or balls falling that you raised in the air (potential energy changing to kinetic energy to "heat"), or hot pans cooling (thermal energy, "heat"), or iron with oxygen changing to iron oxide (bond energy, enthalpy), or wood burning in oxygen (bond energy, enthalpy), each change involves some or all of its energy dispersing to the surroundings. (In cases like a gas expanding into a vacuum, it's the gas's initial energy being spread out more in the new larger volume without any change in the amount of energy, but that energy is becoming more dispersed in space. Likewise, for ideal gases or liquids that mix spontaneously -- the original energy of each component isn't changed; ; it’s just that each kind of molecule has become separated from similar molecules – that’s having their energies dispersed, more spread out than in the original pure gas or liquid.)

     The second law just summarizes our experience with those spontaneous happenings and millions of others: All kinds of energy spontaneously spread out from where they are localized to where they are more dispersed, if they're not hindered from doing so. The opposite does not occur spontaneously -- you don't see rocks concentrating energy from all the other rocks around them and jumping up in the air, while the ground where they were cools down a little. Same way, you'll never see pans in a cupboard getting red hot by taking energy from the other pans or from the air or the cupboard.

P. Good start on the second law. Almost as good as secondlaw.com/two.html. Now go to that big one, "What is entropy, really?"

S: Entropy is no mystery or complicated idea. Entropy is merely the way to measure the energy that disperses or spreads out in a process (at a specific temperature). What's complicated about that? Entropy change, S, measures how much energy is dispersed in a system, or how widely spread out the energy of a system becomes (both always involving T). The first example in our text was melting ice to water at 273 K where S = q(rev)/T. So, in that equation, it's easy to see that q (the enthalpy of fusion) is how much "heat" energy was spread out in the ice to change it to water. What's the big deal?

P. But if entropy measures energy spreading out, and that is q, why bother to divide it by T?

S: Aw, come on. You're trying to see if I really understand! The definition I just told you has to include energy spreading out "at a specific temperature, T" and that means q/T for any reversible process like melting ice (a phase change at a particular temperature, the melting point.)

P: Good work! And as we talked in secondlaw.com/six.html, that simple dividing by T is amazingly important. It's what makes entropy so POWERFUL in helping us understand why things happen in the direction that they do. Let's take the example of a big hot pan as a system that is cooling and let's say q is just a little bit of thermal energy ("heat") that is spreading out from the pan. Let's write the pan's temperature as a bold T to show it is a slightly higher temp than the room. Then..

S: Not that old hot pan again! I'm going to go to sleep on that one.

P: Better not -- look out for the trick coming up!..As the pan cools just a little bit (in a room that is just a little cooler than the pan -- so that temperatures of both pan and room are practically unchanged, and thus the process of heat transfer is a 'reversible' process in the system), the entropy change in the pan is -q/T . But if the change is "minus q over T" that means a decrease of entropy in the system, and yet the pan is spontaneously cooling down! How can that be? Spontaneous events occur only when energy spreads out and entropy increases .yes?

S: Ha -- you can't catch me on that! You're making a mistake by only talking about the system, the pan. That whole process of a pan cooling down doesn't just involve the pan -- it wouldn't cool at all if the surroundings of the pan were at exactly the same T as the pan! So, in this case you have to include the slightly cooler surroundings to which the thermal energy ("heat") is moving, in order to see really what's going on in terms of entropy change. Sure, the pan decreases in entropy but the cooler air of the room increases more in entropy.

P: Very good. You're not sleepy at all. In many processes and chemical reactions, we can just focus on the system (especially as you'll see later in 2ndlaw.com/gibbs.html) and its "free energy" change will tell us whether a process happens spontaneously. But if you see some process in a system that is spontaneous and the system decreases in entropy (for example, what your textbook calls an endothermic chemical reaction that goes spontaneously) look out! Include the surroundings when thinking about what's happening and you'll always find that the surroundings are increasing more in entropy. System plus surroundings. System plus surroundings. Always include both in your thinking, even though you may focus just on one.

Now, let's get back to the hot pan -- and I'll ask something that seems to be too obvious, because you've already mentioned the surrroundings.. There's still a hard question here: Can you scientifically predict why the pan will cool down in a cool room, assuming nothing but knowledge of the second law?

S: Scientifically? Why bother? Everybody knows something hot will cool down in a cool room. Foolish question.

P: I said tell me why, prove to me why! Don't play dumb and say what "everybody knows". The second law tells us that energy spreads out, if it's not hindered from doing so. What's the hindrance to thermal energy ("heat") flowing from the room to the pan or the pan to the room? How can you prove -- on paper, not in an experiment, not by asking "everybody" -- in what direction that "heat" energy will spread out? Only entropy can tell you that, and do it only because of its combination of q/T!

Here are the facts: The thermal energy we're talking about is q. The temperatures are a somewhat larger T in the hot pan system than the smaller T in the cooler room surroundings. Finally, energy spreading out is shown --and measured by -- an increase in entropy of the system plus the surroundings (That combination is called ‘the universe’ in many chemistry texts.)

So the question is, "In which direction is there an increase in entropy in this ‘universe’  of hot pan (q/T) and cooler room (q/T)"? (As you can see from the larger size of T compared to T, q/T is a smaller number than q/T.) Would the energy spread out from the cool room ( surroundings) to the hot pan ( system)? If so, the entropy change would be q/T (pan, system) - q/T (room, surroundings) -- subtraction of a bigger number, q/T, from a smaller number, q/T, yielding a negative number, and a decrease in entropy! That's your directional indicator.  An overall decrease in entropy means that the reaction or process will not go in that direction  spontaneously..

How about q spreading out from the hot pan (systeml) to cooler room (surroundings)? That would be q/T (room) - q/T (pan) -- which equals a positive number, an increase in entropy and therefore its characteristic of a spontaneous process. That's how you can prove what will happen even if you've never seen it happen.

S: OK, OK, I got that. Sometimes we can look only at the system, but we should always keep an eye on the surroundings, i.e., never forget the combo of system plus surroundings! Now, what's that big new stuff about entropy you promised me?

P: I want to talk about MOLECULAR thermodynamics. How the energetic behavior of molecules helps us easily understand what causes entropy change. We'll start by looking at how molecules move, their three kinds of motion. Then we'll see how the total motional energy of a system is spread out among those kinds. Finally, we'll be able to talk about the simple method of measuring entropy change, by the change in the numbers of ways in which the system's energy can be spread out. e.g., in more ways when a gas expands or gases and liquid mix, and also in more ways when anything is heated or a solid changes to a liquid and liquid to a gas or in spontaneous chemical reactions.

S: THREE kinds of motion? I thought molecules just moved, period.

P: Molecules like water, with three or more atoms, not only can (1) whiz around in space and hit each other ("translation", t) but also (2) rotate around axes ("rotation", r) and (3) vibrate along the bonds between the atoms ("vibration", v). Here's a Figure that shows how water can rotate and vibrate.

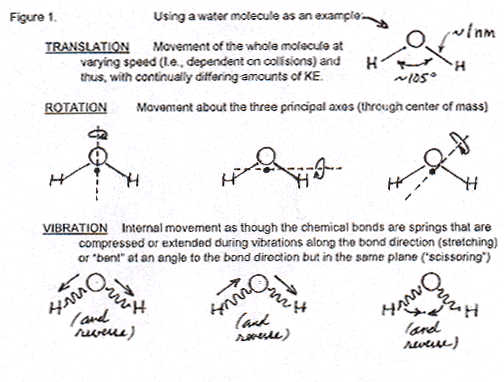
      When you heat any matter, you are putting energy in its molecules and so they move. Of course, in solids, the only possible molecular motion is an extremely small amount of translation. They really just vibrate in place, trillions of times a second. (That's the whole molecule moving but, before it really gets anywhere, almost instantly colliding with molecules next to it that are doing the same thing, not the kind of vibration inside the molecules that is shown in Figure 1.) Neither rotation of molecules or vibration along their bonds can occur freely in solids -- only in liquids and gases. But before we see what comes next, I have to ask you a question, "What do you remember about quantization of energy, and about quantized energy levels?"

S: Ho Ho!! Now I get the chalk again to answer a question! First, I know that all energy, whether the energy that molecules have when moving or light radiation that zings through space, is not continuous. It's actually always in bunches, separate packages, "quanta" of energy rather than like a continuous flow. That's quantization of energy. In units not something continuous like a river.

      And those bunches or quanta are also on quantized energy levels? Do you mean like that electron in a hydrogen atom where it ordinarily can only be at one energy level (i.e., cannot possibly be in-between levels)? But it can be kicked up to a higher energy level by some exact amount of energy input, the right sized "quantum". Only certain energy levels are possible for electrons in a hydrogen atom, the difference between any two levels is therefore quantized. Steps rather than like a continuous slope or a ramp.

P: Good. Now I'll draw a Figure to show the differences in energy levels for the motions in molecules -- like water and those more complex. At the left in the Figure below is the energy "ladder" for vibrations inside the molecules, along their bonds. There's a very large difference between energy levels in vibration. Therefore, large quanta that are only available at high temperatures of many hundreds of degrees to change molecules from the lowest vibrational state to the next higher and so on up. (Essentially all liquid water molecules and most gas phase water would be in the lowest vibrational state, the lowest vibrational level in this diagram.) Then, just to the right of vibrational energy levels is the ladder of rotational levels (with a slightly darker line on the bottom -- I'll get back to that in a second.). The rotational energy levels are much closer together than vibrational. That means it doesn't take as much energy (not such large quanta of energy input) to make a molecule rotate than to make its atoms stretch their bonds a little in vibration. So, a molecule like water with temperatures rising from 273 K to 373 K can get more and more energy from the surroundings to make it rotate and then faster and faster (quantized in those steps or energy levels) in its three different modes (Figure 1).

      Now to that slightly darker or thicker line at the bottom of the rotational energy ladder. It represents the huge number of energy levels of translational motion. It doesn't take much energy just to make a molecule move fast, and then faster. Thus, the quantized difference in translational energy levels is so small that there many levels extremely close to one another in a diagram like this (which includes rotational and vibrational energy levels). Actually there should be a whole bunch of thick lines, many lines on each one of those rotational levels to show the huge numbers of different translational energies for each different energy of rotation.

At the usual lab temperature, most water molecules are moving around 1000 miles an hour, with some at 0 and a few at 4000 mph at any given instant. Their speeds constantly change as they endlessly and violently collide more than trillions and trillions of times a second. When heated above room temperature, they move faster between collisions when their speed may drop to zero if two moving at the same speed hit head on. The next instant each of those "zero speed" molecules will be hit by another molecule and start whizzing again. In a liquid, they hardly get anywhere before being hit. In a gas they can move about a thousand times the diameter of an oxygen molecule before a collision.

S: So?

P: So now we have the clues for seeing what molecules do that entropy measures! First, the motions of molecules involve energy, quantized on specific energy levels. Second, as does any type of energy spread out in its particular kind of energy levels, the energy of molecular motion spreads out as much as it can on its t, r, and v levels.

("As much as it can" means that, with any given energy content, as indicated by a temperature of 298 K (25.0° C), let's say, a mole of water molecules just doesn't have enough energy for any significant number of them to occupy the higher and highest energy levels of vibration or rotation, or even of translation at many thousands of miles an hour.

We say that those levels are "not accessible" under those conditions of T, V and pressure. At any moment (because each molecule's energy is constantly changing due to collisions) all the molecules have enough energy to be in, i.e., to access, the very lowest energy levels. Most can access the mid-energy levels, and some the slightly higher energy levels but there are many higher energy levels that are not accessible until the molecules are given larger quanta of energy when the system is heated.

A simple summary for ordinary systems would be: The most probable distribution of the enormous numbers of molecular energies in a mole, let's say, on various levels is a broad spread among all accessible levels but with more in the average to lower levels than in the higher. [Diagrams of these kinds of "Boltzmann distributions" and how they are calculated are in physical chemistry textbooks.]

S: That was "First", molec motion as quantized energy. Then, spreading out of that energy to accessible energy levels was "second". OK, What's "third"?

P: Third is the beginning of the big payoff. Imagine that you could take an instantaneous snapshot of the energy of all the individual molecules in a flask containing a mole of gas or liquid at 298 K. Remember that each molecule's energy is quantized on a particular energy level. Then, each of the far-more-than Avogadro's number of accessible energy levels (at that temperature and in that volume) could have zero, one, or many many molecules in it or "on it". The whole snapshot showing each molecule's energy of that mole is called a microstate - the exact distribution on energy levels of the energies of all the molecules of the mole at one instant in time.

S: Aw, that's impossible!

P: You're right. It's so impossible that it's ridiculous -- to take that kind of a snapshot. But it's not only possible to think about that concept, it is essential to do it!. The idea of a microstate is the start to a good understanding how molecules are involved in entropy. (And you know well that entropy change is the basis for understanding spontaneous change in the world.)

Since a collision between even two molecules will almost certainly change the speed and thus the energy of each one, they will then be on different energy levels than before colliding. Thus, even though the total energy of the whole mole doesn't change - and even if no other movement occurred - that single collision will change the energy distribution of its system into a new microstate! Because there are trillions times trillions of collisions per second in liquids or gases (and vibrations in solids), a system is constantly changing from one microstate to another, one of the huge number of accessible microstates for any particular system.

S: No change in the total energy of the mole (or whatever amount you start with), but constantly fast-changing so far as the exact distribution of each molecule's energy on one of those gazillion energy levels - each 'exact distribution' being a different microstate?.

P: Ya got it.

S: But what do all those microstates have to do with entropy, if anything?

P: IF ANYTHING?! You're just trying to get me to yell at you :-). Certainly, you don't believe that I'd take all this time talkng about microstates if they weren't extremely important in understanding entropy, do you? OK, here it is: The Boltzmann equation is the relation between microstates and entropy. It states that the entropy of a substance at a given temperature and volume depends on the logarithm of the number of microstates for it,* S = k _B ln (number of microstates), where k_B is the Boltzmann constant of R/N = 1.4 x 10^-23 J/K.. (You will often see W in the Boltzmann equation in textbooks. It stands for " Ways of energy distribution" , the equivalent of the modern term "microstate".) Then, any entropy change from an Initial state to a Final state would be ΔS = k_B ln [(number of microstates)_Final / (number of microstates)_Initial ]

S: Aha! I can predict what you're going to say now: "If the number of microstates for a system (or surroundings) increases, there is going to be an increase in entropy." That's true because the more microstates (Final) the larger the log of whatever the ratio turns out to be and that is multiplied by k_B so the larger will be the ΔS.

P: You're right. Hang in there and you'll be an expert!

S: Thanks, but I still have plenty of questions. What has this to do with what you said that was the fundamental idea about entropy - that energy spontaneously changes from where it is localized to where it becomes more dispersed and spread out. What does "more microstates" for a system have to do with its energy being more spread out? A system can only be in ONE microstate at one time.

P: Yes in only one microstate at one instant. However, the fact that the system has more ‘choices’ or chances of being in more different microstates in the NEXT instant – if there are "more microstates for the system" – is the equivalent of being "more spread out" or "dispersed" instead of staying in a few and thus being localized. (Of course, the greatest localization would be for a system to have only one microstate. That’s the situation at absolute zero T – because then ln W = ln 1 = 0,). To see how the idea of energy dispersal works in thinking about exactly what molecules do just as well as it works on the macro or "big scale beaker" level, let's first summarize the molecular level. Then, let's check four important examples of entropy change to see how energy dispersal occurs on both macro and molecular scales.

You already stated the most important idea, a single microstate of a system has all the energies of all the molecules on specific energy levels at one instant. In the next instant, whether just one collision or many occur, the system is in a different microstate. Because there are a gigantic number of different accessible microstates for any system above 0 K, there are a very large number of choices for the system to be in that next instant. So it is obvious that the greater the number of possible microstates, the greater is the possibility that the system isn't in this one or that one of all of those 'gazillions'. It is in this sense that the energy of the system is more dispersed when the number of possible microstates is greater - there are more choices in any one of which the energy of the system might be at one instant = less possibility that the energy is localized or found in one or just a dozen or only a million microstates. It is NOT that the energy is ever dispersed "over" or "smeared over" many more microstates! That's impossible.

So, what does "energy becomes more dispersed or spread out" mean so far as molecular energies are concerned? Simple! What's the absolute opposite of being dispersed or spread out? Right -- completely localized. In the case of molecular energy, it would be staying always in the same microstate. Thus, having the possibility of a huge number of additional microstates in any one of which all the system's energy might be in -- that's really "more dispersed" at any instant! That's what "an increase in entropy on a molecular scale" is.

S: That's the summary? It would help if you tell me how it applies to your four basic examples of entropy increase on big-scale macro and on molecular levels.

P: First, macro (that you know very well already): Heating a system causes energy from the hot surroundings to become more dispersed in that cooler system. Simplest possible macro example: a warm metal bar touching a slightly cooler metal bar. The thermal energy flows from the warmer to the cooler; it becomes more spread out, dispersed. Or an ice cube in your warm hand: The thermal energy from your hand becomes more dispersed when it flows into the cold ice cube. In both these cases, the entropy of the system is q/T (where T the slightly lower temp) minus the entropy of the surroundings, q/T (where bold T is the higher temperature). That means (larger ΔS_System - smaller ΔS_Surroundings) and therefore, ΔS overall involves an increase in entropy. Energy has become more spread out or dispersed in the ‘universe’ (of system plus surroundings) because of the process of warming a cooler system.

(Students in classes where the quantitative aspects of entropy using q/T are not taught can still grasp the concept of energy becoming dispersed when a system is heated and thus, entropy increasing. The plot of the numbers of molecules having different molecular speeds at low and at high temperatures is shown in most general chemistry textbooks. (Molecular speeds are directly related to molecular energies by mv²/2.) The curve that we see in such plots is actually drawn along the tops of ‘zillions’ of vertical lines, each line representing the speed of a number of molecules. At low temperatures, the plot for those speeds is a fairly high smooth "mountain" down toward the left of the plot. That means that most of the molecules have speeds /energies that are in a relatively small range as shown by the majority of them being under that ‘mountain curve’. At higher temperatures, the "mountain" has become flattened, i.e., molecules have a much broader range of different speeds, far more spread out in their energies rather than being not too different in being ‘crowded together under the mountain’ of the lower temperature curve. Thus, the definition of entropy as a measure or indicator of the greater dispersal of energy is visibly demonstrated by the plots. When a system is heated, its total energy becomes much more spread out in that its molecules have a far greater range in their energies due to that additional thermal energy input. The system's entropy has increased. It, the system, was the cooler ‘object’ when it was heated by a flame or a hot plate; thus, it increased in entropy more than the flame or hot plate decreased.)

The conclusion is the same from another molecular viewpoint. There are many many more microstates for a warmer object or a flame than for a cooler object or substance. However, the transfer of energy to a cooler object causes a greater number of additional microstates to become accessible for that cooler system than the number of microstates that are lost for the hotter system. So, just considering the increase in the number of microstates for the cooler system gives you a proper measure of the entropy increase in it via the Boltzmann equation. Because there are additional accessible microstates for the final state, there are more choices for the system at one instant to be in any one of that larger number of microstates – a greater dispersal of energy on the molecular scale.

S: Heating a system. That's one big example. Now for the second? 

P: The second big category of entropy increase isn’t very big, but often poorly described in general chemistry texts as "positional" entropy (as though energy dispersal had nothing to do with the change and the molecules were just in different ‘positions’!) It involves spontaneous increase in the volume of a system at constant temperature. A gas expanding into a vacuum is the example that so many textbooks illustrate with two bulbs, one of which contains a gas and the other is evacuated. Then, the stopcock between them is opened, the gas expands. In such a process with ideal gases there is no energy change; no heat is introduced or removed. From a macro viewpoint, without any equations or complexities, it is easy to see why the entropy of the system increases: the energy of the system has been allowed to spread out to twice the original volume. It is almost the simplest possible example of energy spontaneously dispersing or spreading out when it is not hindered.

From a molecular viewpoint, quantum mechanics shows that whenever a system is permitted to increase in volume, its molecular energy levels become closer together. Therefore, any molecules whose energy was within a given energy range in the initial smaller-volume system can access more energy levels in that same energy range in the final larger-volume system: Another way of stating this is "The density of energy levels (their closeness) increases when a system's volume increases." Those additional accessible energy levels for the molecules' energies result in many more microstates for a system when its volume becomes larger. More microstates mean many many more possibilities for the system's energy to be in any one microstate at an instant, i.e., an increase in entropy occurs due to that volume change. That's why gases spontaneously mix and why they expand into a vacuum or into lower pressure environments.

S: OK. Heating a system for one, and a gas expanding for two. What’s the third example of basic processes involving entropy change from a macro viewpoint and then a molecular one?

P: The third category isn’t talked about much in some general chemistry texts, but it’s enormously important — mixing or simply "putting two or more substances together". It is not the mixing process itself that causes spontaneous entropy increase and is responsible for spontaneous mixing of ‘like’ liquids or mixing (dissolving) of many solids and liquids. Rather, it is just the separation of one kind of molecule from others of its kind that occurs when liquids are mixed or a solute is added to a pure solvent. that is the source of greater entropy for substances in a mixture. The motional energy of the molecules of each component is more dispersed in a solution than is the motional energy of those molecules in the component’s pure state.

[One rather different case of entropy in mixtures is that of two or more ideal gases. Mixing such gases could be considered as gas expansion that I mentioned a minute ago because one volume of gas A plus one of B makes an increase in volume of both. Thus, this is a clear example of the energy of each gas having its energy spread out to a greater volume and therefore that is the cause of an increase in the entropy of each. However, calculations using the techniques from statistical mechanics that are mentioned two paragraphs below give the same results as those based on simple volume change.]

When liquids are mixed to form a solution, the entropy change in each is not obviously related to a volume change, nor is this true in the most important case of ideal solutes dissolving in solvents. (Dissolving real salts in water involves three energy factors, the separation of ions, the reaction of ions with water, and the dispersal of the energy of the ions in the solution. The latter factor is related to entropy change.) From the macro viewpoint, the entropy increase in forming a solution from a non-ionic solid and a solvent can only be described as due to having two substances present in a solution (hardly an explanation!) and thus, quantitatively, the maximal entropy change in mixing occurs when the concentration of each component in moles is 0.5 of the total number of moles.

From a molecular viewpoint, the calculation and explanation of entropy change in forming a solution from A and B liquids (or A as an ideal solute and B as the solvent) is not as simple as those we have considered. (It is derived in statistical mechanics.) The calculation of entropy change comes from the number of different ‘cells’ (that are actually microstates) that can be formed from combinations of A and B. Far more such cells or microstates are possible from A and B than of the pure substances A or B. Thus, the increase in the ‘combinatoric’ number of cells or microstates as compared to the pure A or B is the basis for calculation of the entropy of the mixture. A solvent in a solution has many more microstates for its energy, and has increased in entropy compared to the pure solvent. Thus, there is less tendency for a solvent to escape from the solution to its vapor phase when heated or to its solid phase when cooled than does the pure solvent. This is the basis of all colligative effects: higher boiling points, lower freezing points, and greater osmotic pressure than the pure solvent.

The elevation of the boiling point of a solvent in a solution? A solvent in a solution has its energy more dispersed in the solution than the pure solvent. Therefore, at the pure solvent’s normal boiling point, not enough solvent molecules tend to escape from the solution to equal the atmospheric pressure and the solution does not ‘boil’. More thermal energy (more ‘heat’) must be forced into the solution to cause more molecules to be able to escape (i.e., it has to be heated to a higher temperature than the pure solvent’s boiling point) for the solvent molecules to overcome the fact that their energy has become more spread out in the solution.

The freezing point of a solvent in a solution? As above, the solvent’s energy is more spread out in the solution than when it was a pure solvent, and so at the pure solvent’s normal freezing point, there is less tendency for the solvent molecules to leave the solution and form the intermolecular bonds of a solid. Cooling to a lower temperature than the pure solvent’s freezing point, causes energy to flow to the colder surroundings and the solvent molecules’ energy to be less dispersed, more localized, more prone to form intermolecular bonds, i.e., to freeze.

Osmotic pressure? The phenomenon of solvent molecules moving through semi-permeable membranes (those thin films that allow solvent molecules to pass through them but obstruct the flow of ions or large molecules) is fundamentally important in biology. Pure solvent that is on one side of a semi-permeable membrane will flow through the membrane if there is a solution on the other side because the result would be an increase in the pure solvent’s entropy -- a spontaneous process. .

S: Now for the fourth example of basic processes – what's the entropy change in them from a macro viewpoint and then a molecular one?

This illustration of entropy change and its equation may be the first equation you see in your text for the concept. It's the original (1865 and still valid) equation of ΔS = q(rev)/T. The calculation is easy but the explanation is impossible without some knowledge of what is occurring on a molecular level.

(Basic lack of knowledge about molecules was the reason that those unfortunate words "order" and "disorder" started to be used in the 1890s to describe entropy change. Leading chemists of that day actually did not believe that molecules existed as real particles. Virtually nothing was known about chemical bonds. Boltzmann believed in the reality of molecules but thought that they might be nearly infinitesimal in size. Thus, in 1898 for people to talk about entropy change in a crystalline material like ice to fluid water as "order" to "disorder" was totally excusable. But with the discovery of the nature of molecules, of chemical bonding, of quantum mechanics and the motional energy of molecules as quantized by 1950, "order" and "disorder" are inexcusable in describing entropy today. See order_to_disorder.pdf.)

From a molecular viewpoint of phase change, e.g., from solid ice to liquid water, we should first see what is occurring in the molecules. The large amount of thermal energy input, the enthalpy of fusion, causes breaking of intermolecular hydrogen bonds in the solid but the temperature stays at 273.15 K. Therefore, the motional energy of molecules in the new liquid water is the same quantity as the molecules that were each vibrating violently in one place in the crystal lattice. The difference is that now molecules in the water are not held so rigidly in the structure of ice. Of course, at 273.16 K (!), they are not zooming around as they would if they were in the gas form, but though they are all jumbled together (and hydrogen -bonded – remember: ice-cold liquid water is more dense than ice), they are extremely rapidly breaking their H bonds and forming new ones (at trillionths of a second rate). So maybe they could be compared to a fantastically huge crowded dance in which the participants hold hands momentarily, but rapidly break loose to grab other hands (OK, H-bonds!) in loose circles many more than billions of times a second. Thus, that initial motional energy of vibration (at 273.14 K!) that was in the crystal is now distributed among an enormous additional number of translational energy levels.

S: All right. You dazzle me with those hydrogen bonds of the ice broken and a zillion other ‘breaks and makes’ going on in the liquid, but what happened to all your talk about microstates being important?

P: Hang in there. I'm just a step ahead of you. Because there are so many additional newly accessible energy levels due to the water molecules being able to break, make, AND move a bit, that means that there are far more additional accessible microstates. Now, maybe you can take over.

S: Sure. Additional accessible microstates mean that at any instant — a trillionth of a trillionth of a second — the total energy of the system is in just one microstate but it has very many more choices for a different microstate the next instant than without "additional accessible microstates". More choices are equivalent to energy being more dispersed or spread out and greater energy dispersal means that the system of liquid water has a larger entropy value than solid water, ice.

P: Good response. Just for fun, I'll show you numbers for what "additional accessible microstates" means.

The standard state entropy of any substance, S⁰, is really S⁰ because it is the entropy change from 0 K to 298 K (or to 273.15 K, in the case of ice.) When we look in the Tables, we find that the S⁰ for a mole of ice is 41 joules/K. So, using the Boltzmann equation, S⁰ = 41 J/K = k_B ln [microstates_{273 K} / 1 ]. Now, since k_B = 1.4 x 10 ^-23 J/K, 41/1.4 x 10 ^-23 = ln microstates _{273 K} . You're probably more comfortable using log₁₀ base rather than natural logarithms. Therefore, let's convert that result for the ln of the microstates to logs by multiplying by 0.43 to give the log of the number of microstates for ice as 0.43 x 2.9 x 10²⁴ or 1.3 x 10²⁴. Wait a minute, you're used to seeing Avogadro's number, N, as 6 x 10²³ but we're now talking about a number that is raised to a power that is more than that, 1.3 x 10²⁴.

      The energy in a cube of ice is constantly being redistributed - in any one of a humanly incomprehensible large numbers of ways, microstates. From the above calculation via the Boltzmann equation, there are 10 ^{1,300,000,000,000,000,000,000,000} microstates for "orderly" crystalline ice, with the energy of the ice in only in one microstate at one instant. Do you see now why it is not wise to talk about "order" and entropy in ice compared to "disorderly" water? What could be more disorderly than that incredible mess for ice of not just trillions times trillions times trillions times trillions of microstates (i.e., which would be only 10 ⁴⁸ !) but 10 ^{1,300,000,000,000,000,000,000,000} ? (There are only about 10 ⁷⁰ particles in the entire universe!)

Now let's calculate how many microstates there are for water -- in any one of which that "disorderly" water can possibly distribute its energy at 273.15 K. At that temperature, water's S⁰ is 63 J/K. Going through the same calculations as above, we find that there are 10 ^{2,000,000,000,000,000,000,000,000} microstates for water. How about that? Yes, water has more possibilities than ice - the liquid system could distribute its energy to any one of more microstates -- (and thus we can say that its energy is more "spread out" than that of ice). But certainly, this is not convincing evidence of a contrast between "disorder" and "order"! We can't have any concept of what these huge numbers mean; we can only write them on paper and manipulate them.

Even though there are more microstates for water at 273,15 K than for ice, the difference between 2.0 and 1.3 times 10 ^{1,000,000,000,000,000,000,000,000} is surely not convincing evidence of a contrast between "disorder" and "order". "Disorder" in relation to entropy is an obsolete notion and has been discarded by most new editions of US general chemistry texts. (See cracked_crutch.html and also scroll down to April 2007 in entropysite.com/#whatsnew)

A qualitative statement of the second law of thermodynamics

Energy of all types spontaneously flows from being localized or concentrated to becoming more dispersed or spread out, if it is not hindered.

The generalization for classical thermodynamics (macro thermo, Clausius):

               Entropy change measures either (1) how much molecular motional energy has been spread out in a reversible process divided by the temperature increments, e.g., ΔS = q_rev /T, or (2) how spread out in space the original motional energy becomes without any chance in thetemperature, e.g., ΔS = R ln V₂/V₁ as in the expansion of a gas into a vacuum.

                (1) could involve heating a system very very gently (i.e., so the temperature stays just barely above the original system temperature, nearly reversibly) by energy being transferred from the hotter surroundings such as a flame or a hot plate to the cooler system. (In irreversible heating (i..e ,.to any temperature large or small above what the system is originally ), the entropy change can be calculated by simulating tiny reversible steps via calculus: C_p /T dT.
               (2) involves expansion of a gas into a vacuum, mixing of gases or of liquids, and dissolving solids in liquids because the energy of the rapidly moving gas molecules or the mobile molecules of each constituent in a mixture literally become more spread out in if they move to occupy a larger three-dimensional volume. At the same time (and theoretically very important) the motional energy of each constituent’s molecules is actually spread out in the sense of having the chance of being, at one instant, in any one of many many more different arrangements on energy levels in the larger gas volume or in a mixture than each had access to before the process of expansion or of mixing.

The generalization for molecular thermodynamics (micro thermo, (Boltzmann):

Entropy measures the energy dispersal for a system by the number of accessible microstates, the number of arrangements (each containing the total system energy) for which the molecules' quantized energy can be distributed, and in one of which – at a given instant – the system exists prior to changing to another.
S = k_B ln [Microstates_final/Microstates_initial]

Entropy is not a driving force.

Energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. The overall process is an increase in thermodynamic entropy, enabled in chemistry by the motional energy of molecules (or the energy from bond energy change in a reaction) and actualized because the process makes available a larger number of microstates, a maximal probability. . (See ConFigEntPublicat.pdf , a September 2007 article.)

The two factors, energy and probability, are both necessary for thermodynamic entropy change but neither is sufficient alone. In sharp contrast, information ‘entropy’ depends only on the Shannon H, and ‘sigma entropy’ in physics (σ = S/k_B) depends only on probability as ln W.

Entropy is not "disorder". [See cracked_crutch.html ]

Entropy is not a "measure of disorder".

Disorder in macro objects is caused by energetic agents (wind, heat, earthquakes, driving rain, people, or, in a quite different category, gravity) acting on them to push them around to what we see as "disorderly" arrangements, their most probable locations after any active agent has moved them. The agents (other than gravity!) undergo an increase in their entropy in the process. The objects are unchanged in entropy if they are simply rearranged.

Even though breaking a mole-sized crystal of NaCl in half involves slight changes in hundreds to thousands of the NaCl units adjacent to the fracture line, in addition to those actually on such a line, there are still at least 10⁶ bonds totally unaffected. Thus we can see why a single fracture of a ski (unhappy as it is to the skier), or a house torn apart in to ten thousand pieces by a hurricane (disastrous as it is to the homeowner), represent truly insignificant entropy changes. [shakespeare2ndlaw.com] The only notable scientific entropy change occurs in the agent causing the breaks. Human concepts of order are misplaced in evaluating entropy.

        Professor John P. Lowe's explanation of the importance of the occupancy of energy levels as a genuine basis for entropy (rather than "randomness" or "disorder") via informal QandA is in the Journal of Chemical Education, 1988, 65 (5), 403 - 406. Pages 405 and 406 are especially pertinent and very readable.

        An excellent introduction to Professor Norman C. Craig's procedure of attacking entropy problems is in "Entropy Analyses of Four Familiar Processes", Journal of Chemical Education, 1988, 65 (9), 760 - 764. Professor Craig's 200 page paperback Entropy Analysis (John Wiley, New York, 1992), is the best short technical introduction to the laws of thermodynamics and the correct utilization of entropy in print. It is accessible to a diligent first-year college student, and especially valuable to a student beginning physical chemistry thermo (as well as to mature chemists who really never understood entropy in their thermodynamics classes).

        Most 2005 and later editions of US college general chemistry texts have discarded the use of "disorder" in connection with entropy. Three or four still present entropy as coming in "two flavors", "positional" entropy and "thermal" entropy. (There is only one kind of entropy change: plain vanilla, measured by dq(rev)/T on a macro level, or on the molecular level by the change in the number of microstates after vs. before a process, by the Boltzmann entropy equation. This is shown in a September 2007 article in JChemEduc at ConFigEntPublicat.pdf. "Positional entropy" ignores the fact that its calculation of particulate volume increase from statistical mechanics also fundamentally counts microstates, not just ‘cells’ of location or volume in space. Microstates are the accessible arrangements for a system’s energy, not arrangements of its molecules in space.

• secondlaw.com, mentioned in this section, is a practical introduction to the second law from which illustrations in this present site were taken, but the treatment of entropy there emphasizes macro thermodynamics except for an introduction of molecular thermodynamics in the Appendix.
• Shuffled Cards, Messy Desks, and Disorderly Dorm Rooms shows why shuffled cards, messy desks and disorderly dorm rooms are NOT examples of entropy increase: Journal of Chemical Education, 1999, 76 (10), 1385 - 1387.
• "Disorder -- A Cracked Crutch For Supporting Entropy Discussions" shows that "disorder" is an archaic, misleading description of entropy for chemistry students. It should be replaced by the simple description of entropy as a measure of the dispersal or spreading out of molecular motional energy in a process (as a function of temperature).
• Entropy is not “disorder” is a more formal presentation of the concepts in this site for instructors. "Entropy Is Simple, Qualitatively" presents the material in this site more formally.
• entropysite.com/#articles includes the foregoing articles and seven other letters and articles that use the approach of this site.

Please forward any good tutorial thermo URLs that you find so they can be listed here.

Home     Next page - "The second law of thermodynamics is a tendency"